题目内容
【题目】如图，正方形ABCD边长为4，点P从点A运动到点B，速度为1，点Q沿B﹣C﹣D运动，速度为2，点P、Q同时出发，则△BPQ的面积y与运动时间t（t≤4）的函数图象是（ ）
A.
B.
C.
D.
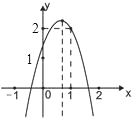
【答案】B
【解析】①点P在AB上运动，点Q在BC上运动，即0≤t≤2，
此时AP=t，BP=4﹣t，QB=2t，
故可得y= 
PBQB= （4﹣t）2t=﹣t2+4t，函数图象为开口向下的抛物线；
②点P在AB上运动，点Q在CD上运动，即2＜t≤4
此时AP=t，BP=4﹣t，△BPQ底边PB上的高保持不变，为正方形的边长4，
故可得y= BP×4=﹣2t+8，函数图象为直线．
综上可得全过程的函数图象，先是开口向下的抛物线，然后是直线；
所以答案是：B．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
练习册系列答案
相关题目
