题目内容
【题目】顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地，甲出发0.5h后乙开始出发，结果比甲早1（h）到达B地，如图，线段OP、MN分别表示甲、乙两车离A地的距离S（km）与时间t（h）的关系，a表示A、B两地之间的距离．请结合图中的信息解决如下问题：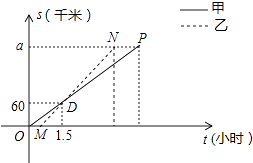 
（1）分别计算甲、乙两车的速度及a的值；
（2）乙车到达B地后以原速立即返回，请问甲车到达B地后以多大的速度立即匀速返回，才能与乙车同时回到A地？并在图中画出甲、乙两车在返回过程中离A地的距离S（km）与时间t（h）的函数图象．
【答案】
（1）解：由图象得：甲的速度为：60÷1.5=40（km/h），
乙的速度为：60÷（1.5﹣0.5）=60（km/h），
求a的方法如下：
方法1：由题意得： 
= 
﹣1﹣0.5，解得：a=180；
方法2：设甲到达B地的时间为t时，则乙所用的时间为（t﹣1﹣0.5）时，
由题意得：40t=60（t﹣1﹣0.5），
t=4.5，
∴a=40t=40×4.5=180，
答：甲、乙两车的速度分别为40km/h、60km/h，a的值是180km
（2）解：方法1：设甲返回时的速度为xkm/h，
则 
= 
，
解得：x=90，
经检验：x=90是原方程的解，用符合题意，
所以，甲返回时的速度为90km/h；
方法2：甲、乙同时返回A地，则甲返回时所用的时间为： 
=2，
所以，甲返回时的速度为：180÷2=90（km/h）．
图象如图所示：
【解析】（1）根据路程÷时间计算甲、乙两车的速度；介绍两种计算a的方法：
方法1：根据乙的时间=甲的时间列方程可得a的值；
方法2：设甲到达B地的时间为t时，则乙所用的时间为（t﹣1﹣0.5）时，根据甲的路程=乙的路程列方程可得t的值，从而可以计算a的值（a=40t）；（2）方法1：设甲返回时的速度为xkm/h，根据时间相等列分式方程，注意要检验；
方法2：利用算术法列式计算：先根据乙的时间得甲返回时的时间比乙少用一个小时： 
﹣1；则甲的速度是：180÷2，可得结论，
根据甲去时的时间为4.5h，可得一共所用的时间为：4.5+2=6.5h，画图．
【考点精析】本题主要考查了函数的图象的相关知识点，需要掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能正确解答此题．
