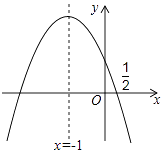ΧβΡΩΡΎ»ί
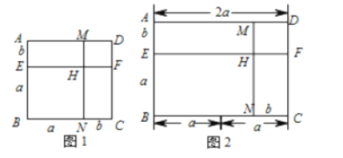
ΓΨΧβΡΩΓΩ»γΆΦ1 «“ΜΗω»ΐάβ÷υΑϋΉΑΚ–Θ§ΥϋΒΡΒΉΟφ «±Ώ≥ΛΈΣ10cmΒΡ’ΐ»ΐΫ«–ΈΘ§»ΐΗω≤ύΟφΕΦ «ΨΊ–ΈΘ°œ÷ΫΪΩμΈΣ15cmΒΡ≤ …ΪΨΊ–Έ÷Ϋ¥χAMCN≤ΟΦτ≥…“ΜΗωΤΫ––ΥΡ±Ώ–ΈABCDΘ®»γΆΦ2Θ©Θ§»ΜΚσ”Ο’βΧθΤΫ––ΥΡ±Ώ–Έ÷Ϋ¥χΑ¥»γΆΦ3ΒΡΖΫ ΫΑ―’βΗω»ΐάβ÷υΑϋΉΑΚ–ΒΡ≤ύΟφΫχ––ΑϋΧυΘ®“Σ«σΑϋΧυ ±ΟΜ”–÷ΊΒΰ≤ΩΖ÷Θ©Θ§÷Ϋ¥χ‘Ύ≤ύΟφ≤χ»Τ»ΐ»ΠΘ§’ΐΚΟΫΪ’βΗω»ΐάβ÷υΑϋΉΑΚ–ΒΡ≤ύΟφ»Ϊ≤ΩΑϋΧυ¬ζΘ°‘ΎΆΦ3÷–Θ§ΫΪ»ΐάβ÷υ―ΊΙΐΒψAΒΡ≤ύάβΦτΩΣΘ§ΒΟΒΫ»γΆΦ4ΒΡ≤ύΟφ’ΙΩΣΆΦΘ°ΈΣΝΥΒΟΒΫ≤ΟΦτΒΡΫ«Ε»Θ§Έ“Ο«Ω…“‘ΗυΨί’ΙΩΣΆΦΤ¥Ϋ”≥ωΖϊΚœΧθΦΰΒΡΤΫ––ΥΡ±Ώ–ΈΫχ––―–ΨΩΘ°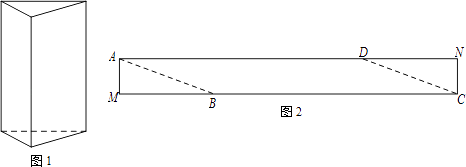
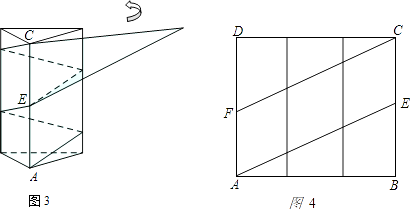
Θ®1Θ©«κ‘ΎΆΦ4÷–Μ≠≥ωΤ¥Ϋ”ΚσΖϊΚœΧθΦΰΒΡΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©«κ‘ΎΆΦ2÷–Θ§ΦΤΥψ≤ΟΦτΒΡΫ«Ε»Θ®Φ¥ΓœABMΒΡΕ» ΐΘ©Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ»γΆΦΥυ ΨΘΚ
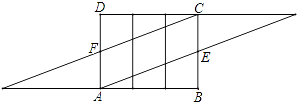
Θ®2Θ©ΫβΘΚ”…ΆΦ2ΒΡΑϋΧυΖΫΖ®÷ΣΘΚABΒΡ≥ΛΒ»”Ύ»ΐάβ÷υΒΡΒΉ±Ώ÷ή≥ΛΘ§
ΓύAB=30Θ°
ΓΏ÷Ϋ¥χΩμΈΣ15Θ§
ΓύsinΓœABM= ![]() Θ§
Θ§
ΓύΓœABM=30ΓψΘ°
ΓΨΫβΈωΓΩΘ®1Θ© Ήœ»ΫΪΆΦ4÷–ΒΡΓςABEœρΉσΤΫ“Τ30cmΘ§»ΜΚσ‘ΌΫΪΓςCDFœρ”“ΤΫ“Τ30cmΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίABΒΡ≥ΛΒ»”Ύ»ΐάβ÷υΒΡΒΉ±Ώ÷ή≥ΛΩ…«σΒΟAB=30cmΘ§”…÷Ϋ¥χΒΡΩμΈΣ15cmΘ§ΉνΚσΘ§“άΨίΧΊ β»ώΫ«»ΐΫ«Κ· ΐ÷ΒΩ…«σΒΟΓœAMB=30Γψ.
ΓΨΩΦΒψΨΪΈωΓΩΫβ¥π¥ΥΧβΒΡΙΊΦϋ‘Ύ”ΎάμΫβΦΗΚΈΧεΒΡ’ΙΩΣΆΦΒΡœύΙΊ÷Σ ΕΘ§’ΤΈ’―ΊΕύΟφΧεΒΡάβΫΪΕύΟφΧεΦτΩΣ≥…ΤΫΟφΆΦ–ΈΘ§»τΗ…ΗωΤΫΟφΆΦ–Έ“≤Ω…“‘Έß≥…“ΜΗωΕύΟφΧεΘΜΆ§“ΜΗωΕύΟφΧε―Ί≤ΜΆ§ΒΡάβΦτΩΣΘ§ΒΟΒΫΒΡΤΫΟφ’ΙΩΣΆΦ «≤Μ“Μ―υΒΡΘ§ΨΆ «ΥΒΘΚΆ§“ΜΗωΝΔΧεΆΦ–ΈΩ…“‘”–Εύ÷÷≤ΜΆ§ΒΡ’ΙΩΣΆΦΘ§“‘ΦΑΕ‘ΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΒΡάμΫβΘ§ΝΥΫβΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘±ΏœύΒ»«“ΤΫ––ΘΜΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘Ϋ«œύΒ»Θ§ΝΎΫ«ΜΞ≤ΙΘΜΤΫ––ΥΡ±Ώ–ΈΒΡΕ‘Ϋ«œΏΜΞœύΤΫΖ÷Θ°

 Οϊ Π÷ΗΒΦΤΎΡ©≥ε¥ΧΨμœΒΝ–¥πΑΗ
Οϊ Π÷ΗΒΦΤΎΡ©≥ε¥ΧΨμœΒΝ–¥πΑΗ