题目内容
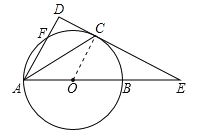
【题目】如图,AB是⊙O的直径,直线CD与⊙O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
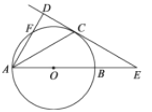
(1)求证:AD⊥CD;
(2)若∠CAD=30°.⊙O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,![]() ≈1.73,结果保留一位小数.)
≈1.73,结果保留一位小数.)
【答案】(1)证明见解析;(2)11.3
【解析】
(1)连接OC,根据切线的性质得到OC⊥CD,证明OC∥AD,根据平行线的性质证明;
(2)根据圆周角定理得到∠COE=60°,根据勾股定理、弧长公式计算即可.
(1)连接OC.
∵直线CD与⊙O相切,∴OC⊥CD.
∵点C是![]() 的中点,∴∠DAC=∠EAC.
的中点,∴∠DAC=∠EAC.
∵OA=OC,∴∠OCA=∠EAC,∴∠DAC=∠OCA,∴OC∥AD,∴AD⊥CD;
(2)∵∠CAD=30°,∴∠CAE=∠CAD=30°,由圆周角定理得:∠COE=60°,∴OE=2OC=6,EC=![]() OC=3
OC=3![]() =
=![]() =π,∴蚂蚁爬过的路程=3+3
=π,∴蚂蚁爬过的路程=3+3![]() +π≈11.3.
+π≈11.3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目