Question

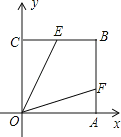
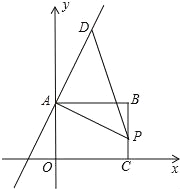
【题目】如图，矩形ABC0位于直角坐标平面，O为原点，A、C分别在坐标轴上，B的坐标为（8，6），线段BC上有一动点P，已知点D在第一象限．

（1）D是直线y＝2x+6上一点，若△APD是等腰直角三角形，求点D的坐标；

（2）D是直线y＝2x﹣6上一点，若△APD是等腰直角三角形．求点D的坐标．

Answer 1

【答案】（1）D（4，14）；（2）（4，2）或（，）或（，）．

【解析】

（1）根据题意可知AD＝AP，作辅助线,证明△ADE≌△PAF（AAS），求得OE,代入函数解析式即可求得D坐标,

（2）分三种情况：当∠ADP＝90°时，D在AB上方和下方,当∠APD＝90°时.设PC=m,分别表示出D点坐标,代入y＝2x﹣6,即可解题,

解；（1）如图1所示，作DE⊥y轴于E点，作PF⊥y轴于F点，可得∠DEA＝∠AFP＝90°，

根据题意可知当△APD为等腰直角三角形时，只有∠DAP＝90°满足条件，

∴AD＝AP，∠DAP＝90°，

∴∠EAD+∠DAB＝90°，∠DAB+∠BAP＝90°，

∴∠EAD＝∠BAP，

∵AB∥PF，

∴∠BAP＝∠FPA，

∴∠EAD＝∠FPA，

在△ADE和△PAF中，

,

∴△ADE≌△PAF（AAS），

∴AE＝PF＝8，OE＝OA+AE＝14，

设点D的横坐标为x，由14＝2x+6，得x＝4，

∴点D的坐标是（4，14）；

（2）由点D在直线y＝2x﹣6上，可设PC＝m，

如图2所示，当∠ADP＝90°时，AD＝PD，易得D点坐标（4，2）；

如图3所示，当∠APD＝90°时，AP＝PD，设点P的坐标为（8，m），

则D点坐标为（14﹣m，m+8），由m+8＝2（14﹣m）﹣6，得m＝，

∴D点坐标（，）；

如图4所示，当∠ADP＝90°时，AD＝PD时，

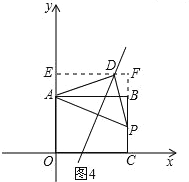
同理可求得D点坐标（，），

D点坐标分别为（4，2）或（，）或（，）．