题目内容
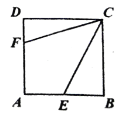
【题目】如图,正方形![]() 的边长为12,点
的边长为12,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,若
上,若![]() ,且
,且![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
首先延长FD到G,使DG=BE,利用正方形的性质得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性质易证△GCF≌△ECF,利用勾股定理可得DF,求出AF,设BE=x,利用GF=EF,解得x,再利用勾股定理可得CE.
解:如图,延长FD到G,使DG=BE;
连接CG、EF;
∵四边形ABCD为正方形,
在△BCE与△DCG中,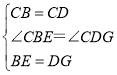 ,
,
∴△BCE≌△DCG(SAS),
∴CG=CE,∠DCG=∠BCE,
∴∠GCF=45°,
在△GCF与△ECF中,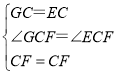 ,
,
∴△GCF≌△ECF(SAS),
∴GF=EF,
∵DF=![]() ,AB=AD=12,
,AB=AD=12,
∴AF=124=8,
设BE=x,则AE=12x,EF=GF=4+x,
在Rt△AEF中,由勾股定理得:(12x)2+82=(4+x)2,
解得:x=6,
∴BE=6,
∴CE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目