题目内容
【题目】如图,在矩形ABCD中,AB=5cm,BC=2cm,M,N两点分别从A,B两点以2cm/s和1cm/s的速度在矩形ABCD边上沿逆时针方向运动,其中有一点运动到点D即停止,当运动时间为_____秒时,△MBN为等腰三角形.

【答案】![]() 或(6-2
或(6-2![]() )或
)或![]()
![]()
【解析】
分情况讨论:①点M在AB上,点N在BC上时,BM=BN,列出方程其解即可;②点M在BC上,点N在CD上时,表示出BM、CM、CN,再根据勾股定理列式表示出MN2,然后根据BM=MN列出方程求解即可;③点M、N都在C、D上时,表示出MN、CM,再根据勾股定理分两种情况列式表示出BM(或BN),然后根据BM=MN(或BN=MN)列出方程求解即可;④点M在AB上,点N在CD上时,根据等腰三角形的性质,CN=![]() BM,然后列式求解即可.
BM,然后列式求解即可.
解:分情况讨论:
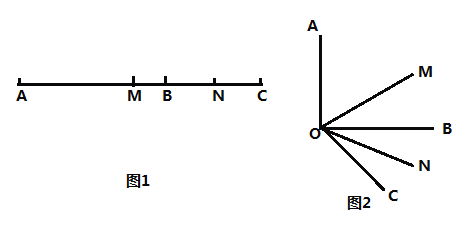
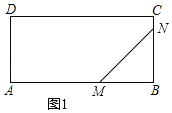
①如图1所示:
点M在AB上,点N在BC上时,t<2,BM=5﹣2t,BN=t,
∵BM=BN,
∴5﹣2t=t,
解得t=![]() ;
;
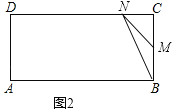
②如图2所示:
点M在BC上,点N在CD上时,2.5<t<3.5,BM=2t﹣5,CM=2﹣(2t﹣5)=7﹣2t,CN=t﹣2,
在Rt△MCN中,MN2=(7﹣2t)2+(t﹣2)2,
∵BM=MN,
∴(2t﹣5)2=(7﹣2t)2+(t﹣2)2,
整理得,t2﹣12t+28=0,
解得:t1=6﹣2![]() ,t2=6+2
,t2=6+2![]() (舍去);
(舍去);
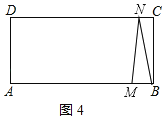
③如图3所示:
点M、N都在C、D上时,t>3.5,
若点M在点N的右边,则CM=2t﹣7,MN=t﹣(2t﹣7)=7﹣2t,
此时BM2=(2t﹣7)2+22,
∵BM=MN,
∴(2t﹣7)2+22=(7﹣2t)2,无解,
若点M在点N的左边,则CN=t﹣2,MN=(2t﹣7)﹣(t﹣2)=t﹣5,
此时BN2=(t﹣2)2+22,
∵BN=MN,
∴(t﹣2)2+22=(t﹣5)2,
整理得,t=![]() (不符合题意,舍去),;
(不符合题意,舍去),;
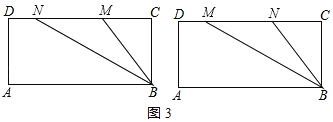
④如图4所示:
点M在AB上,点N在CD上时,BM=5﹣2t,CN=t﹣2,
由等腰三角形三线合一的性质,CN=![]() BM,
BM,
∴t﹣2=![]() (5﹣2t),
(5﹣2t),
解得:t=![]() ;
;
综上所述,当运动时间为![]() 或(6﹣2
或(6﹣2![]() )或
)或![]() 秒时,△MBN为等腰三角形.
秒时,△MBN为等腰三角形.
故答案为:![]() 或(6﹣2
或(6﹣2![]() )或
)或![]() .
.

【题目】某儿童游乐园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 13元 | 11元 | 9元 |
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1218元.问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?
(3)如果七年级(1)班有10名学生因学校有任务不能参加这次旅游,请你为两个班设计出购买门票的方案,并指出最省钱的方案.