ЬтФПФкШн
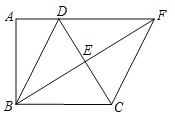
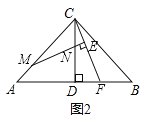
ЁОЬтФПЁПШчЭМЃКвбжЊЁїABCжаЃЌCA=CBЃЌCDЁЭABгкDЕуЃЌЕуMЮЊЯпЖЮACЩЯвЛЖЏЕуЃЌЯпЖЮMNНЛDCгкЕуNЃЌЧвЁЯBAC=2ЁЯCMNЃЌЙ§ЕуCзїCEЁЭMNНЛMNбгГЄЯпгкЕуEЃЌНЛЯпЖЮABгкЕуFЃЌЬНЫї![]() ЕФжЕ.
ЕФжЕ.
ЃЈ1ЃЉШєЁЯACB=90ЁуЃЌЕуMгыЕуAжиКЯЃЈШчЭМ1ЃЉЪБЃКЂйЯпЖЮCEгыEFжЎМфЕФЪ§СПЙиЯЕЪЧ ЃЛЂк![]() = ЃЛ
= ЃЛ
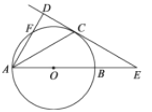
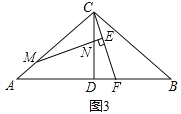
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШєЕуMВЛгыЕуAжиКЯЃЈШчЭМ2ЃЉЃЌЧыВТЯыаДГі![]() ЕФжЕЃЌВЂжЄУїФуЕФВТЯы
ЕФжЕЃЌВЂжЄУїФуЕФВТЯы
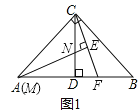
ЃЈ3ЃЉШєЁЯACBЁй90ЁуЃЌЁЯCAB=![]() ЃЌЦфЫћЬѕМўВЛБфЃЌЧыжБНгаДГі
ЃЌЦфЫћЬѕМўВЛБфЃЌЧыжБНгаДГі![]() ЕФжЕЃЈгУКЌга
ЕФжЕЃЈгУКЌга![]() ЕФЪНзгБэЪОЃЉ
ЕФЪНзгБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉЂйCE=EFЃЌЂк ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() =
=![]() ЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ
ЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ![]() =
=![]() .
.
ЁОНтЮіЁП(1)ЁЂИљОнЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛЖЈРэЕУГіЕуEЮЊCFЕФжаЕуЃЌДгЖјЕУГіД№АИЃЛ(2)ЁЂЙ§ЕуMзїMQ//ABНЛCDгкЕуPЃЌНЛCFгкЕуQЃЌИљОнЕШбќШ§НЧаЮЁЂжБНЧШ§НЧаЮЕФаджЪЕУГіЁїMPNКЭЁїCPQШЋЕШЃЌДгЖјЕУГіCE=EQ ЃЌMC=MQЃЌМДCE=![]() CQ=
CQ=![]() MNЃЛ(3)ЁЂШчЭМ3ЃЌЭЌ(1)ЁЂ(2)ПЩЕУCE=
MNЃЛ(3)ЁЂШчЭМ3ЃЌЭЌ(1)ЁЂ(2)ПЩЕУCE= ![]() CQЃЌвзжЄЁїMPN~ЁїCPQЃЌдђга
CQЃЌвзжЄЁїMPN~ЁїCPQЃЌдђга![]() ЃЌМД
ЃЌМД![]() ЃЎ
ЃЎ
(1)ЁЂЂйCE=EFЃЛЂк ![]() ЃЛ
ЃЛ
(2)ЁЂ![]() =
=![]()
РэгЩШчЯТЃКШчЭМ2ЫљЪОЃКЙ§ЕуMзїMQ//ABНЛCDгкЕуPЃЌНЛCFгкЕуQЃЌ
дђгаЁЯCMP=ЁЯBAC=45ЁуЃЌ ЁрCP=MPЃЌ
ЁпЁЯBAC=2ЁЯCMNЃЌ ЁрЁЯCMP=2ЁЯCMNЃЌ ЁрЁЯCMN=ЁЯNMP=22.5ЁуЃЌЁпCEЁЭMNЃЌ
ЁрЁЯCEM=ЁЯQEM=90ЁуЃЌЁрCE=EQ ЃЈШ§ЯпКЯвЛЃЉЃЌЁпCDЁЭABЃЌ MQ//ABЃЌ
ЁрCDЁЭMQЃЌЁрЁЯMPN=ЁЯCPQ=90ЁуЃЌгжЁпЁЯNCE+ЁЯCNE=ЁЯNCE+ЁЯCQN=90ЁуЃЌ
ЁрЁЯCQN=ЁЯCNE=ЁЯMNPЃЌгжCP=MPЃЌЁрЁїMPN![]() ЁїCPQЃЌЁрCE=EQ ЃЌMC=MQЃЌ
ЁїCPQЃЌЁрCE=EQ ЃЌMC=MQЃЌ
ЁрCE=![]() CQ=
CQ=![]() MNЃЌЁр
MNЃЌЁр![]() =
=![]() ЃЛ
ЃЛ
(3)ЁЂ![]() =
=![]() ЃЎ
ЃЎ
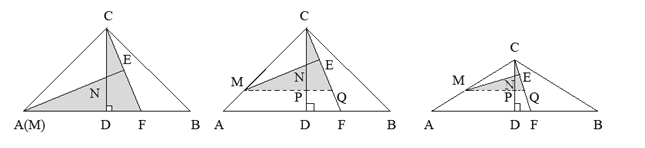
ЭМ1 ЭМ2 ЭМ3

ЁОЬтФПЁПФГЖљЭЏгЮРждАУХЦБМлИёЙцЖЈШчЯТБэЃК
ЙКЦБеХЪ§ | 1~50еХ | 51~100еХ | 100еХвдЩЯ |
УПеХЦБЕФМлИё | 13дЊ | 11дЊ | 9дЊ |
ФГаЃЦпФъМЖЃЈ1ЃЉЁЂЃЈ2ЃЉСНИіАрЙВ102ШЫНёФъ6ЃЎ1ЖљЭЏНкШЅгЮИУгЮРждАЃЌЦфжаЃЈ1ЃЉАрШЫЪ§НЯЩйЃЌВЛзу50ШЫЃЎОЙРЫуЃЌШчЙћСНИіАрЖМвдАрЮЊЕЅЮЛЙКЦБЃЌдђвЛЙВгІИЖ1218дЊЃЎЮЪЃК
ЃЈ1ЃЉСНИіАрИїгаЖрЩйбЇЩњЃП
ЃЈ2ЃЉШчЙћСНАрСЊКЯЦ№РДЃЌзїЮЊвЛИіЭХЬхЙКЦБЃЌПЩвдНкЪЁЖрЩйЧЎЃП
ЃЈ3ЃЉШчЙћЦпФъМЖЃЈ1ЃЉАрга10УћбЇЩњвђбЇаЃгаШЮЮёВЛФмВЮМгетДЮТУгЮЃЌЧыФуЮЊСНИіАрЩшМЦГіЙКТђУХЦБЕФЗНАИЃЌВЂжИГізюЪЁЧЎЕФЗНАИЃЎ