ЬтФПФкШн
ЁОЬтФПЁПШєвЛИіЫФБпаЮЕФвЛЬѕЖдНЧЯпАбЫФБпаЮЗжГЩСНИіЕШбќШ§НЧаЮЃЌЮвУЧАбетЬѕЖдНЧЯпНаетИіЫФБпаЮЕФКЭаГЯпЃЌетИіЫФБпаЮНазіКЭаГЫФБпаЮЃЎШчСтаЮОЭЪЧКЭаГЫФБпаЮЃЎ

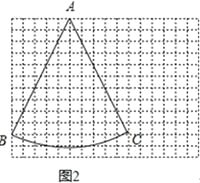
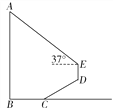
ЃЈ1ЃЉШчЭМ1ЃЌдкЬнаЮABCDжаЃЌADЁЮBCЃЌЁЯBAD=120ЁуЃЌЁЯC=75ЁуЃЌBDЦНЗжЁЯABCЃЎЧѓжЄЃКBDЪЧЬнаЮABCDЕФКЭаГЯпЃЛ
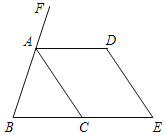
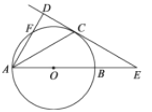
ЃЈ2ЃЉШчЭМ2ЃЌдк12ЁС16ЕФЭјИёЭМЩЯЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЉгавЛИіЩШаЮBACЃЌЕуAЃЎBЃЎCОљдкИёЕуЩЯЃЌЧыдкД№ЬтОэИјГіЕФСНИіЭјИёЭМЩЯИїеввЛИіЕуDЃЌЪЙЕУвдAЁЂBЁЂCЁЂDЮЊЖЅЕуЕФЫФБпаЮЕФСНЬѕЖдНЧЯпЖМЪЧКЭаГЯпЃЌВЂЛГіЯргІЕФКЭаГЫФБпаЮЃЛ
ЃЈ3ЃЉЫФБпаЮABCDжаЃЌAB=AD=BCЃЌЁЯBAD=90ЁуЃЌACЪЧЫФБпаЮABCDЕФКЭаГЯпЃЌЧѓЁЯBCDЕФЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЁЯBCDЕФЖШЪ§ЮЊ135ЁуЛђ90ЁуЛђ45Ёу.
ЁОНтЮіЁП
ЃЈ1ЃЉвЊжЄУїBDЪЧЫФБпаЮABCDЕФКЭаГЯпЃЌжЛашвЊжЄУїЁїABDКЭЁїBDCЪЧЕШбќШ§НЧаЮМДПЩ.
ЃЈ2ЃЉИљОнЩШаЮЕФаджЪЛЁЩЯЕФЕуЕНЖЅЕуЕФОрРыЯрЕШЃЌжЛвЊDдк![]() ЩЯШЮвтвЛЕуЙЙГЩЕФЫФБпаЮABDCОЭЪЧКЭаГЫФБпаЮЃЛСЌНгBCЃЌдкЁїBACЭтзївЛИівдACЮЊбќЕФЕШбќШ§НЧаЮACDЃЌЙЙГЩЕФЫФБпаЮABCDОЭЪЧКЭаГЫФБпаЮ.
ЩЯШЮвтвЛЕуЙЙГЩЕФЫФБпаЮABDCОЭЪЧКЭаГЫФБпаЮЃЛСЌНгBCЃЌдкЁїBACЭтзївЛИівдACЮЊбќЕФЕШбќШ§НЧаЮACDЃЌЙЙГЩЕФЫФБпаЮABCDОЭЪЧКЭаГЫФБпаЮ.
ЃЈ3ЃЉгЩACЪЧЫФБпаЮABCDЕФКЭаГЯпЃЌПЩвдЕУГіЁїACDЪЧЕШбќШ§НЧаЮЃЌДгЭМ4ЃЌЭМ5ЃЌЭМ6Ш§жжЧщПідЫгУЕШБпШ§НЧаЮЕФаджЪЃЌе§ЗНаЮЕФаджЪКЭ30ЁуЕФжБНЧШ§НЧаЮаджЪОЭПЩвдЧѓГіЁЯBCDЕФЖШЪ§.
ЃЈ1ЃЉЁпADЁЮBCЃЌЁрЁЯABC+ЁЯBAD=180ЁуЃЌЁЯADB=ЁЯDBC.
ЁпЁЯBAD=120ЁуЃЌЁрЁЯABC=60Ёу.
ЁпBDЦНЗжЁЯABCЃЌЁрЁЯABD=ЁЯDBC=30Ёу.
ЁрЁЯABD=ЁЯADB.ЁрЁїADBЪЧЕШбќШ§НЧаЮ.
дкЁїBCDжаЃЌЁЯC=75ЁуЃЌЁЯDBC=30ЁуЃЌЁрЁЯBDC=ЁЯC=75Ёу.ЁрЁїBCDЮЊЕШбќШ§НЧаЮ.
ЁрBDЪЧЬнаЮABCDЕФКЭаГЯп.
ЃЈ2ЃЉгЩЬтвтзїЭМЮЊЃКЭМ2ЃЌЭМ3
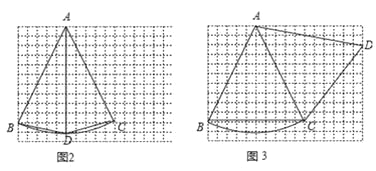
ЃЈ3ЃЉЁпACЪЧЫФБпаЮABCDЕФКЭаГЯпЃЌЁрЁїACDЪЧЕШбќШ§НЧаЮ.
ЁпAB=AD=BCЃЌЁрЗжШ§жжЧщПіЃК
ШчЭМ4ЃЌЕБAD=ACЪБЃЌ
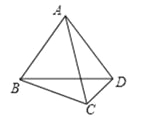
ЭМ4
ЁрAB=AC=BCЃЌЁЯACD=ЁЯADC.
ЁрЁїABCЪЧе§Ш§НЧаЮ.ЁрЁЯBAC=ЁЯBCA=60Ёу.
ЁпЁЯBAD=90ЁуЃЌЁрЁЯCAD=30Ёу.
ЁрЁЯACD=ЁЯADC=75Ёу.ЁрЁЯBCD=60Ёу+75Ёу=135Ёу.
ШчЭМ5ЃЌЕБAD=CDЪБЃЌ
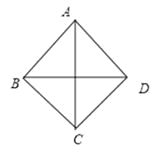
ЭМ5
ЁрAB=AD=BC=CD.
ЁпЁЯBAD=90ЁуЃЌЁрЫФБпаЮABCDЪЧе§ЗНаЮ.
ЁрЁЯBCD=90Ёу.
ШчЭМ6ЃЌЕБAC=CDЪБЃЌ
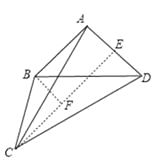
ЭМ6
Й§ЕуCзїCEЁЭADгкEЃЌЙ§ЕуBзїBFЁЭCEгкFЃЌ
ЁпAC=CDЃЎCEЁЭADЃЌЁрAE=ADЃЌЁЯACE=ЁЯDCE.
ЁпЁЯBAD=ЁЯAEF=ЁЯBFE=90ЁуЃЌ
ЁрЫФБпаЮABFEЪЧОиаЮ.ЁрBF=AE.
ЁпAB=AD=BCЃЌЁрBF=BC.ЁрЁЯBCF=30Ёу.
ЁпAB=BCЃЌЁрЁЯACB=ЁЯBAC.
ЁпABЁЮCEЃЌЁрЁЯBAC=ЁЯACE.ЁрЁЯACB=ЁЯACE=ЁЯBCF=15Ёу.
ЁрЁЯBCD=15ЁуЁС3=45Ёу.
злЩЯЫљЪіЃЌЁЯBCDЕФЖШЪ§ЮЊ135ЁуЛђ90ЁуЛђ45Ёу.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ