题目内容
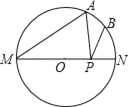
【题目】已知二次函数y=ax2+bx+c(a>0)经过点M(﹣1,2)和点N(1,﹣2),交x轴于A,B两点,交y轴于C.则:
①b=﹣2;
②该二次函数图象与y轴交于负半轴;
③存在这样一个a,使得M、A、C三点在同一条直线上;
④若a=1,则OAOB=OC2 .
以上说法正确的有( )
A. ①②③④ B. ②③④ C. ①②④ D. ①②③
【答案】C
【解析】①∵二次函数y=ax2+bx+c(a>0)经过点M(1,2)和点N(1,2),
∴![]() ,
,
解得b=2.故该选项正确;
②由①可得b=2,a+c=0,即c=a<0,
所以二次函数图象与y轴交于负半轴.
故该选项正确;
③根据抛物线图象的特点,M、A.C三点不可能在同一条直线上.故该选项错误;
④当a=1时,c=1,∴该抛物线的解析式为y=x22x1
当y=0时,0=x22x+c,利用根与系数的关系可得x1x2=c,
即OAOB=|c|,
当x=0时,y=c,即OC=|c|=1=OC2
∴若a=1,则OAOB=OC2,
故该选项正确.
总上所述①②④正确.
故选:C.

练习册系列答案
相关题目