题目内容
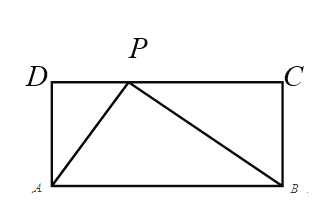
【题目】如图，正方形ABCD的对角线相交于点O，点E，F分别是边BC上两点，且
.将
绕点O逆时针旋转，当点F与点C重合时，停止旋转.已知，BC=6，设BE=x，EF=y.
小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程，请补充完整：
(1)按照下表中自变量x的值进行取点、画图、测量，得到了y与x的几组对应值；
x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
y | 3 | 2.77 | 2.50 | 2.55 | 2.65 |
(说明：补全表格时相关数值保留一位小数)
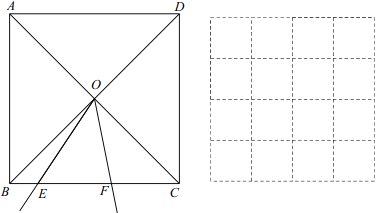
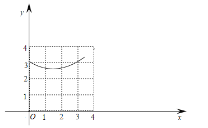
(2)建立平面直角坐标系，描出补全后的表中各对对应值为坐标的点，画出该函数的图象；
(3)结合函数图象，解决问题：当EF=2BE时，BE的长度约为______.
【答案】(1)2.6，3；(2)见解析；(3)1.26.
【解析】
（1）在AB上截取BM=FC=6－x－y，连接ME，OM，由“SAS”可证△BMO≌△CFO，△EOF≌△EOM，可得ME=EF，由勾股定理可得
，可得y=
（0≤x≤6），将x=1，x=3代入可求解.
（2）利用描点法画出图形即可解决问题.
（3）由题意可得y=2x，代入y与x的关系式可求BE的值．
（1）如图，在AB上截取BM=FC=6－x－y，连接ME，OM，∵四边形ABCD是正方形，
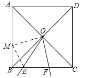
∴BO=CO=AO=DO，∠ABD=∠ACB=45°，且BM=CF，∴△BMO≌△CFO（SAS），∴OM=OF，∠BOM=∠COF，∵∠EOF=45°，∴∠BOE+∠COF=45°，∴∠BOM+∠BOE=45°=∠MOE，∴∠MOE=∠EOF，且OF=OM，OE=OE，∴△EOF≌△EOM（SAS）∴ME=EF∵BM+BE=ME=EF，∴x+（6-x-y）=y，∴y=（0≤x≤6）∴当x=1，y=2.6，当x=3，y=3；故答案为2.6，3.
（2）
(3) ∵EF=2BE，∴y=2x，∴2x=，∴x=
≈1.26；故答案为1.26
