题目内容
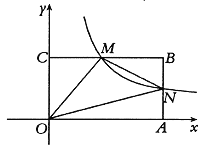
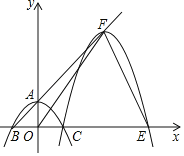
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一交点为E,其顶点为F.
(1)求a、c的值;
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
【答案】(1)a=![]() ,c=2;(2)△OEF为等腰三角形,理由见解析
,c=2;(2)△OEF为等腰三角形,理由见解析
【解析】
(1)根据△ABC为等腰直角三角形可以得出 OA=OB=OC=c,从而得出S△ABC=![]() ,据此求出c的值,然后进一步得出C点坐标,接着将其代入解析式求出
,据此求出c的值,然后进一步得出C点坐标,接着将其代入解析式求出![]() 的值即可;
的值即可;
(2)设抛物线向右平移m个单位,则向上平移m个单位,则点F(m,m+2),则新抛物线的表达式为:y=![]() (xm)2+m+2,将点C的坐标代入上式进一步分析证明即可.
(xm)2+m+2,将点C的坐标代入上式进一步分析证明即可.
(1)∵△ABC为等腰直角三角形,∴OA=OB=OC=c,
故S△ABC=![]() ,
,
解得:![]() 或
或![]() (舍去),
(舍去),
故点C的坐标分别为:(2,0),
将点C的坐标代入y=![]() x2+2并解得:
x2+2并解得:
![]() ,
,
故![]() ,c=2;
,c=2;
(2)根据题意,设抛物线向右平移m个单位,则向上平移m个单位,
则点F(m,m+2),
∴新抛物线的表达式为:y=![]() (xm)2+m+2,
(xm)2+m+2,
将点C的坐标代入上式得:0=![]() (2m)2+m+2
(2m)2+m+2
解得:m=0(舍去)或6,
则函数的对称轴为x=m=6,
∴点F坐标为:(6,8),则点E(10,0),而点O(0,0),
则OF2=![]() ,OE2=100,EF2=
,OE2=100,EF2=![]() ,
,
即OF=OE,
∴△OEF为等腰三角形.

练习册系列答案
相关题目