题目内容
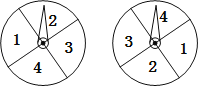
【题目】学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是_____.
【答案】![]()
【解析】
先通过列表列举出所有情况,再求出两指针指的数字之积为偶数的情况占总情况的多少即可.
解:根据题意列表如下;
积 | 1 | 2 | 3 | 4 |
1 | 1 | 2 | 3 | 4 |
2 | 2 | 4 | 6 | 8 |
3 | 3 | 6 | 9 | 12 |
4 | 4 | 8 | 12 | 16 |
所有出现的等可能情况有16种,积为偶数的有12种情况,
所以两指针所指数字的积为偶数的概率是![]() ,
,
所以乙获胜的概率为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】如图,正方形ABCD的对角线相交于点O,点E,F分别是边BC上两点,且![]() .将
.将![]() 绕点O逆时针旋转,当点F与点C重合时,停止旋转.已知,BC=6,设BE=x,EF=y.
绕点O逆时针旋转,当点F与点C重合时,停止旋转.已知,BC=6,设BE=x,EF=y.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值;
x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
y | 3 | 2.77 | 2.50 | 2.55 | 2.65 |
(说明:补全表格时相关数值保留一位小数)
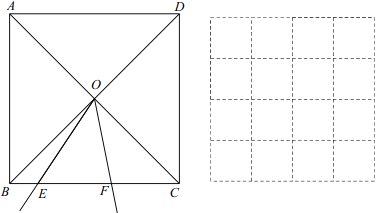
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合函数图象,解决问题:当EF=2BE时,BE的长度约为______.