题目内容
如图,在梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6.求CE的长.


延长AF至BC延长线上交于G点,
∵AD∥BC,
∴△ADF∽△GCF,
∴AF:FG=DF:CF,
∵DF=CF
∴AF=FG.
∵AE=BE,
∴∠ABE=∠BAE,
∵AF⊥AB,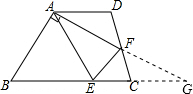
∴∠ABE+∠AGB=90°,∠BAE+∠EAG=90°,
∴∠AGB=∠EAG,
∴AE=EG,
∴GE=BE,
∴E为BG中点,
∴EF是△ABG的中位线,
故可得:EF=
AB=3,FG=AF=4,
∴AG=8,
∴BG=10,
∴EG=5,
∵AF⊥AB,AE=BE,
∴点E是BG的中点,
∴EG=BE=5,
∴可得△EFG为直角三角形,
∴CE=EG-CG=EG-AD=5-2.7=2.3.
∵AD∥BC,
∴△ADF∽△GCF,
∴AF:FG=DF:CF,
∵DF=CF
∴AF=FG.
∵AE=BE,
∴∠ABE=∠BAE,
∵AF⊥AB,

∴∠ABE+∠AGB=90°,∠BAE+∠EAG=90°,
∴∠AGB=∠EAG,
∴AE=EG,
∴GE=BE,
∴E为BG中点,
∴EF是△ABG的中位线,
故可得:EF=
| 1 |
| 2 |
∴AG=8,
∴BG=10,
∴EG=5,
∵AF⊥AB,AE=BE,
∴点E是BG的中点,
∴EG=BE=5,
∴可得△EFG为直角三角形,
∴CE=EG-CG=EG-AD=5-2.7=2.3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



