ƒøƒ⁄»ð
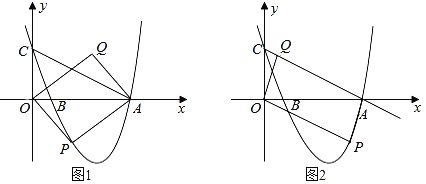
°æƒø°ø»ÁÕº1À˘ 棨≈◊ŒÔœþ![]() ”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨“—÷™Cµ„◊¯±ÍŒ™£®0£¨4£©£¨≈◊ŒÔœþµƒ∂•µ„µƒ∫·◊¯±ÍŒ™
”Îx÷·Ωª”⁄A°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨“—÷™Cµ„◊¯±ÍŒ™£®0£¨4£©£¨≈◊ŒÔœþµƒ∂•µ„µƒ∫·◊¯±ÍŒ™![]() £¨µ„P «µ⁄ÀƒœÛœÞƒ⁄≈◊ŒÔœþ…œµƒ∂ص„£¨Àƒ±þ–ŒOPAQ «∆Ω––Àƒ±þ–Œ£¨…˵„Pµƒ∫·◊¯±ÍŒ™m£Æ
£¨µ„P «µ⁄ÀƒœÛœÞƒ⁄≈◊ŒÔœþ…œµƒ∂ص„£¨Àƒ±þ–ŒOPAQ «∆Ω––Àƒ±þ–Œ£¨…˵„Pµƒ∫·◊¯±ÍŒ™m£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©«Û π°˜APCµƒ√ʪ˝Œ™’˚ ˝µƒPµ„µƒ∏ˆ ˝£ª
£®3£©µ±µ„P‘⁄≈◊ŒÔœþ…œ‘À∂Ø ±£¨Àƒ±þ–ŒOPAQø…ƒÐ «’˝∑Ω–Œ¬£ø»Ùø…ƒÐ£¨«Î«Û≥ˆµ„Pµƒ◊¯±Í£¨»Ù≤ªø…ƒÐ£¨«ÎÀµ√˜¿Ì”…£ª
£®4£©‘⁄µ„QÀʵ„P‘À∂صƒπ˝≥Ã÷–£¨µ±µ„Q«°∫√¬‰‘⁄÷±œþAC…œ ±£¨‘Ú≥∆µ„QŒ™°∞∫Õ–≥µ„°±£¨»ÁÕº£®2£©À˘ 棨«Î÷±Ω”–¥≥ˆµ±QŒ™°∞∫Õ–≥µ„°±µƒ∫·◊¯±Íµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©9∏ˆ £ª£®3£©
£ª£®2£©9∏ˆ £ª£®3£©![]() ªÚ
ªÚ![]() £ª£®4£©
£ª£®4£©![]()
°æΩ‚Œˆ°ø
£®1£©≈◊ŒÔœþ”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨∂•µ„µƒ∫·◊¯±ÍŒ™
£¨∂•µ„µƒ∫·◊¯±ÍŒ™![]() £¨‘Ú
£¨‘Ú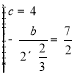 £¨º¥ø…«ÛΩ‚£ª
£¨º¥ø…«ÛΩ‚£ª
£®2£©![]() µƒ√ʪ˝
µƒ√ʪ˝![]() £¨º¥ø…«ÛΩ‚£ª
£¨º¥ø…«ÛΩ‚£ª
£®3£©µ±Àƒ±þ–Œ![]() «’˝∑Ω–Œ ±£¨µ„
«’˝∑Ω–Œ ±£¨µ„![]() ÷ªƒÐ‘⁄
÷ªƒÐ‘⁄![]() ÷·µƒœ¬∑Ω£¨¥À ±
÷·µƒœ¬∑Ω£¨¥À ±![]() Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨…˵„
Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨…˵„![]() £¨‘Ú
£¨‘Ú![]() £¨º¥ø…«ÛΩ‚£ª
£¨º¥ø…«ÛΩ‚£ª
£®4£©«Û≥ˆ÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() £¨‘Ú÷±œþ
£¨‘Ú÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() ¢⁄£¨¡™¡¢¢Ÿ¢⁄«Û≥ˆ
¢⁄£¨¡™¡¢¢Ÿ¢⁄«Û≥ˆ![]() µƒ◊¯±Í£¨”÷Àƒ±þ–Œ
µƒ◊¯±Í£¨”÷Àƒ±þ–Œ![]() «∆Ω––Àƒ±þ–Œ£¨‘Ú
«∆Ω––Àƒ±þ–Œ£¨‘Ú![]() µƒ÷–µ„º¥Œ™
µƒ÷–µ„º¥Œ™![]() µƒ÷–µ„£¨º¥ø…«ÛΩ‚£Æ
µƒ÷–µ„£¨º¥ø…«ÛΩ‚£Æ
Ω‚£∫£®1£©≈◊ŒÔœþ”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨∂•µ„µƒ∫·◊¯±ÍŒ™
£¨∂•µ„µƒ∫·◊¯±ÍŒ™![]() £¨‘Ú
£¨‘Ú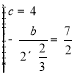 £¨Ω‚µ√
£¨Ω‚µ√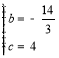 £¨
£¨
π ≈◊ŒÔœþµƒ≈◊ŒÔœþŒ™£∫![]() £ª
£ª
£®2£©∂‘”⁄![]() £¨¡Ó
£¨¡Ó![]() £¨‘Ú
£¨‘Ú![]() ªÚ6£¨π µ„
ªÚ6£¨π µ„![]() °¢
°¢![]() µƒ◊¯±Í∑÷±Œ™
µƒ◊¯±Í∑÷±Œ™![]() °¢
°¢![]() £ª
£ª
»ÁÕº£¨π˝µ„![]() ◊˜
◊˜![]() ÷·Ωª
÷·Ωª![]() ”⁄µ„
”⁄µ„![]() £¨
£¨
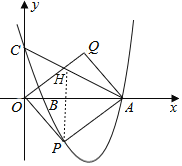
…Ë÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]()
”…µ„![]() £®6£¨0£©°¢
£®6£¨0£©°¢![]() £®0£¨4£©µƒ◊¯±Íµ√
£®0£¨4£©µƒ◊¯±Íµ√![]() £¨Ω‚µ√
£¨Ω‚µ√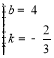 £¨
£¨
°ý÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() ¢Ÿ£¨
¢Ÿ£¨
…˵„![]() £¨‘Úµ„
£¨‘Úµ„![]() £¨
£¨
![]() µƒ√ʪ˝
µƒ√ʪ˝![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() £¨µ±
£¨µ±![]() ±£¨
±£¨![]() £¨
£¨
π π![]() µƒ√ʪ˝Œ™’˚ ˝µƒ
µƒ√ʪ˝Œ™’˚ ˝µƒ![]() µ„µƒ∏ˆ ˝Œ™9∏ˆ£ª
µ„µƒ∏ˆ ˝Œ™9∏ˆ£ª
£®3£©µ±Àƒ±þ–Œ![]() «’˝∑Ω–Œ ±£¨µ„
«’˝∑Ω–Œ ±£¨µ„![]() ÷ªƒÐ‘⁄
÷ªƒÐ‘⁄![]() ÷·µƒœ¬∑Ω£¨
÷·µƒœ¬∑Ω£¨
¥À ±![]() Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨…˵„
Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨…˵„![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨
º¥![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() ªÚ4£¨
ªÚ4£¨
𠵄![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨
£¨![]() ªÚ
ªÚ![]() £ª
£ª
£®4£©…˵„![]() £¨Œ™µ„
£¨Œ™µ„![]() £¨
£¨
…Ë÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() £¨
£¨
”…µ„![]() £¨
£¨![]() µƒ◊¯±Íø…µ√
µƒ◊¯±Íø…µ√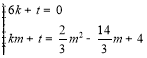 £¨Ω‚÷Ƶ√£∫
£¨Ω‚÷Ƶ√£∫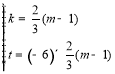
°ý÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() £¨
£¨
![]() £¨‘Ú
£¨‘Ú![]() ∫Õ
∫Õ![]() ±Ì¥Ô Ω÷–µƒ
±Ì¥Ô Ω÷–µƒ![]() ÷µœýÕ¨£¨
÷µœýÕ¨£¨
π ÷±œþ![]() µƒ±Ì¥Ô ΩŒ™£∫
µƒ±Ì¥Ô ΩŒ™£∫![]() ¢⁄£¨
¢⁄£¨
¡™¡¢¢Ÿ¢⁄µ√£∫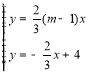 £¨Ω‚µ√£∫
£¨Ω‚µ√£∫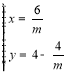 £¨
£¨
‘Úµ„![]() £¨
£¨![]() £¨
£¨
![]() Àƒ±þ–Œ
Àƒ±þ–Œ![]() «∆Ω––Àƒ±þ–Œ£¨‘Ú
«∆Ω––Àƒ±þ–Œ£¨‘Ú![]() µƒ÷–µ„º¥Œ™
µƒ÷–µ„º¥Œ™![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨
»ÁÕº2£¨◊˜![]() ÷·”⁄µ„C£¨
÷·”⁄µ„C£¨![]() ÷·”⁄µ„D£¨
÷·”⁄µ„D£¨
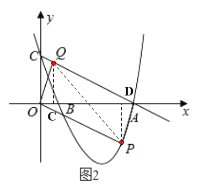
°ý![]() ,
,
‘Ú”–£¨![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £¨
£¨
æ≠ºÏ—È£¨![]() «‘≠∑÷ Ω∑Ω≥õ√∏˙£¨
«‘≠∑÷ Ω∑Ω≥õ√∏˙£¨
‘Ú![]() £¨
£¨
π ![]() µƒ∫·◊¯±Íµƒ÷µŒ™
µƒ∫·◊¯±Íµƒ÷µŒ™![]() £Æ
£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏°æƒø°øŒ™–˚¥´∆’º∞–¬π⁄∑Œ—◊∑¿÷Œ÷™ ∂£¨“˝µº—ß…˙◊ˆ∫√∑¿øÿ£Æƒ≥–£æŸ––¡À÷˜Ã‚Œ™°∞∑¿øÿ–¬π⁄£¨¥”Œ“◊ˆ∆°±µƒœþ…œ÷™ ∂æ∫»¸ªÓ∂Ø£¨≤‚ ‘ƒ⁄»ðŒ™20µ¿≈–∂œÃ‚£¨√øµ¿Ã‚5∑÷£¨¬˙∑÷100∑÷£¨Œ™¡ÀΩ‚∞À°¢æ≈ƒÍº∂—ß…˙¥À¥Œæ∫»¸≥…º®µƒ«Èøˆ£¨∑÷±Àʪ˙‘⁄∞À°¢æ≈ƒÍº∂∏˜≥È»°¡À20√˚≤Œ»¸—ß…˙µƒ≥…º®£Æ“—÷™≥È≤ȵ√µΩµƒ∞ÀƒÍº∂µƒ ˝æð»Áœ¬£∫80£¨95£¨75£¨75£¨90£¨75£¨80£¨65£¨80£¨85£¨75£¨65£¨70£¨65£¨85£¨70£¨95£¨80£¨75£¨80£Æ
Œ™¡À±„”⁄∑÷Œˆ ˝æð£¨Õ≥º∆‘±∂‘∞ÀƒÍº∂ ˝æðΩ¯––¡À’˚¿Ì£¨µ√µΩ¡À±Ì“ª£∫
≥…º®µ»º∂ | ∑÷ ˝£®µ•Œª£∫∑÷£© | —ß…˙ ˝ |
Dµ» | 60£ºx°Ð70 | 5 |
Cµ» | 70£ºx°Ð80 | a |
Bµ» | 80£ºx°Ð90 | b |
Aµ» | 90£ºx°Ð100 | 2 |
æ≈ƒÍº∂≥…º®µƒ∆Ωæ˘ ˝°¢÷–Œª ˝°¢”≈–„¬ »Áœ¬£∫£®∑÷ ˝80∑÷“‘…œ°¢≤ª∫¨80∑÷Œ™”≈–„£©
ƒÍº∂ | ∆Ωæ˘ ˝ | ÷–Œª ˝ | ”≈–„¬ |
∞ÀƒÍº∂ | 77.5 | c | m% |
æ≈ƒÍº∂ | 76 | 82.5 | 50% |
£®1£©∏˘æðƒø–≈œ¢ÃÓø’£∫a£Ω°°°°£¨c£Ω°°°°£¨m£Ω°°°°£ª
£®2£©∞ÀƒÍº∂–°”Ó∫Õæ≈ƒÍº∂–°¿÷µƒ∑÷ ˝∂ºŒ™80∑÷£¨«Î≈–∂œ–°”Ó°¢–°¿÷‘⁄∏˜◊‘ƒÍº∂µƒ≈≈√˚ƒƒŒª∏¸øø«∞£ø«ÎºÚ ˆƒ„µƒ¿Ì”…£ª
£®3£©»Ùæ≈ƒÍº∂π≤”–600»À≤Œº”≤Œ»¸£¨«Îπ¿º∆æ≈ƒÍº∂80∑÷“‘…œµƒ»À ˝£Æ
°æƒø°øæ≈ƒÍº∂ƒ≥∞ý◊º±∏—°∞ŒÀƒ√˚ƒ–…˙≤Œº”—ß–£‘À∂ت·Ω”¡¶±»»¸£¨Ω¯––¡À“ª¥Œ50√◊∂Ã≈Ð≤‚—È£¨≥…º®»Áœ¬£¨(µ•Œª£∫√Î)6.9 7.0 7.1°°7.2°°7.0°°7.4°°7.3°°7.5°°7.0°°7.4 7.3 6.8 7.0°°7.1 7.3 6.9 7.1 7.2 7.4 6.9 7.0 7.2 7.0 7.2 7.6
∞ý÷˜»Œ¿œ ¶∞¥0.2√εƒ◊Èæý∑÷∂Œ£¨Õ≥º∆√ø∏ˆ≥…º®∂Œ≥ˆœ÷µƒ∆µ ˝£¨ÃÓ»Î∆µ ˝∑÷≤º±Ì£¨≤¢ªÊ÷∆¡À∆µ ˝∑÷≤º÷±∑ΩÕº£Æ
≥…º®∂Œ£®√Σ© |
|
|
|
|
|
∆µ ˝ | 4 | 9 | 7 |
| 1 |
Ƶ |
| 0.36 | 0.28 | 0.16 | 0.04 |
£®1£©«Ûa°¢b÷µ£¨≤¢Ω´∆µ ˝∑÷≤º÷±∑ΩÕº≤π≥‰ÕÍ’˚£ª
£®2£©«Îº∆À„’‚¥Œ∂Ã≈Ð≤‚—ȵƒ”≈–„¬ (7.0√κ∞7.0√Γ‘œ¬)£ª
£®3£©≥…º®«∞Àƒ√˚µƒA°¢B°¢C°¢DÕ¨—ß◊È≥…æ≈ƒÍº∂ƒ≥∞ý4°¡100√◊Ω”¡¶∂”£¨∆‰÷–≥…º®◊Ó∫√µƒAÕ¨—ß∞≤≈≈‘⁄◊Ó∫Û“ª∞Ù(µ⁄4∞Ù)£¨¡ÌÕ‚»˝ŒªÕ¨—ßÀʪ˙±ý≈≈‘⁄∆‰”ý»˝∏ˆ∞Ù¥Œ£¨ª≠ ˜◊¥ÕºªÚ¡–±ÌÀµ√˜B°¢C¡ΩŒªÕ¨—ߌ™œý¡⁄∞Ù¥Œµƒ∏≈¬ £Æ