Question

【题目】如图所示，在Rt△ABC中，∠C＝90°，按以下步骤作图：

①以点A为圆心，以小于AC的长为半径作弧，分别交AC、AB于点M，N；

②分别以点M，N为圆心，以大于MN的长为半径作弧，两弧相交于点O；

③作射线OA，交BC于点E，若CE＝6，BE＝10．

则AB的长为（　　）

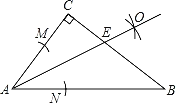
A.11B.12C.18D.20

Answer 1

【答案】D

【解析】

过点E作DE⊥AB于点D，由作图知AP平分∠BAC，根据角平分线的性质得到CE＝DE＝6，根据勾股定理得到BD＝8，根据全等三角形的性质得到AC＝AD，设AC＝AD＝x，根据勾股定理即可得到结论．

解：过点E作DE⊥AB于点D，

由作图知AP平分∠BAC，

∵∠C＝∠ADE＝90°，

∴CE＝DE＝6，

∵BE＝10，

∴BD＝8，

∵AD＝AD，CE＝DE，

∴Rt△ACE≌Rt△ADE（HL），

∴AC＝AD，

设AC＝AD＝x，

由AC2+BC2＝AB2得x2+162＝（x+8）2，

解得：x＝6，即AC＝12，

∴ AB＝20，

故选：D．