题目内容
【题目】平面直角坐标系中,直线l1:![]() 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2:![]() 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
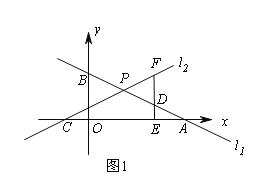
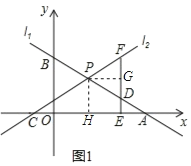
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
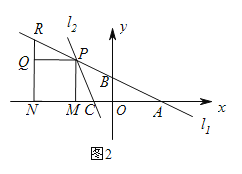
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
【答案】(1)P(![]() ,
,![]() );(2)
);(2)![]() ;(3)(
;(3)(![]() ,
,![]() )
)
【解析】
(1把k=1代入l2解析式,当k=1时,直线l2为y=x+2.与l1组成方程组
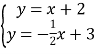 , 解这个方程组得:
, 解这个方程组得:![]() ,
,
∴P(![]() ,
,![]() );
);
(2)当y=0时,kx+2k=0 ,∵k≠0,∴x=-2,
∴C(-2,0),OC=2,当y=0时,-![]() x+3=0,∴x=6,
x+3=0,∴x=6,
∴A(6,0),OA=6 ,
过点P作PG⊥DF于点G,
在△PDG和△ADE中,
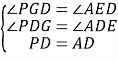
∴△PDG≌△ADE,
得DE=DG=![]() DF,
DF,
∴PD=PF,
∴∠PFD=∠PDF
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°
∴∠PCA=∠PAC,
∴PC=PA
过点P作PH⊥CA于点H,
∴CH=![]() CA=4,
CA=4,
∴OH=2,
当x=2时,y=![]() ×2+3=2代入y=kx+2k,得k=
×2+3=2代入y=kx+2k,得k=![]() ;
;
(3)在Rt△PMC和Rt△PQR中,
![]()
∴Rt△PMC≌Rt△PQR,
∴
∴NR=NC,
设NR=NC=a,则R(a2,a),
代入y=![]() x+3,
x+3,
得![]() (a2)+3=a,解得a=8,
(a2)+3=a,解得a=8,
设P(m,n),则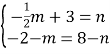
解得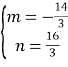
∴P(![]() ,
,![]() )
)

【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.