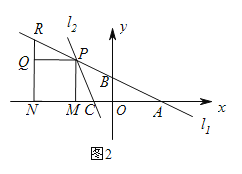
题目内容
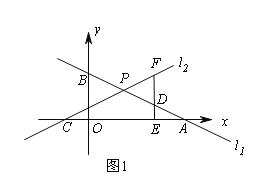
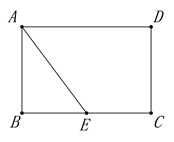
【题目】如图,∠MON=90°,矩形ABCD的顶点C、D分别在边ON,OM上滑动,AB=9,BC=6,在滑动过程中,点A到点O的最大距离为_________.
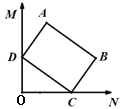
【答案】12.
【解析】
取DC的中点E,连接OE、AE、AO,根据三角形的任意两边之和大于第三边可知当O、A、E三点共线时,点A到点O的距离最大,再根据勾股定理求出AE的长,根据直角三角形斜边上的中线等于斜边的一半求出OE的长,两者相加即可得解.
如图,取DC的中点E,连接OE、AE、OD,
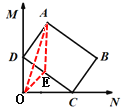
∵OA≤OE+AE,
∴当O、A、E三点共线时,点A到点O的距离最大,
∵四边形ABCD是矩形,
∴DC=AB,AD=BC,
此时,∵AB=9,BC=6,
∴OE=DE=![]() DC=
DC=![]() ,
,
∴AE=![]() ,
,
∴OD的最大值为:![]() +
+![]() =12;
=12;
故答案为:12.

练习册系列答案
相关题目
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.