Question

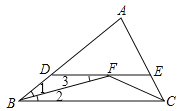
【题目】已知：∠ABC，∠ACB的平分线相交于F点，过点F作DE∥BC，交AB于点D，交AC于点E．

（1）请你写出图中所有的等腰三角形；

（2）请写出BD，CE，DE之间的数量关系；

（3）并对第（2）问中BD，CE，DE之间的数量关系给予证明．

Answer 1

【答案】（1）等腰三角形有：△BDF和△CEF；（2）BD+CE=DE；（3）证明见解析．

【解析】试题分析：（1）结合图形即可得解；

（2）根据等腰三角形的两腰相等即可推出BD+CE=DE；

（3）根据角平分线的定义可得∠1=∠2，再根据两直线平行，内错角相等可得∠2=∠3，然后求出∠1=∠3，再根据等角对等边求出BD=FD，同理可得CE=EF，从而得证．

试题解析：解：（1）等腰三角形有：△BDF和△CEF；

（2）BD+CE=DE；

（3）∵BF平分∠ABC，∴∠1=∠2，∵DE∥BC，∴∠2=∠3，∴∠1=∠3，∴BD=FD，同理可得CE=EF，∴BD+CE=FD+EF=DE，即BD+CE=DE．