题目内容
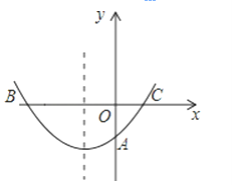
【题目】如图，在平面直角坐标系中，点O为坐标原点，平移抛物线y=x2﹣2x+3，使平移后的抛物线经过点A（﹣2，0），且与y轴交于点B，同时满足以A，O，B为顶点的三角形是等腰直角三角形，求平移后的抛物线的解析式．
【答案】y=x2+3x+2或y=x2+x﹣2
【解析】
利用A点坐标和等腰三角形的性质可求得B点坐标，设出平移后的抛物线的解析式，把A、B的坐标代入可求得平移后的抛物线的解析式．
解：∵点B在y轴上，且△AOB是等腰直角三角形，A（﹣2，0）， ∴点B的坐标为（0，2）或（0，﹣2），
根据题意设平移后抛物线解析式为y=x2+bx+c，
将（﹣2，0）、（0，2）代入得：
，
解得： 
，
∴此时抛物线解析式为y=x2+3x+2；
将（﹣2，0）、（0，﹣2）代入得：
，
解得： 
，
∴此时抛物线解析式为y=x2+x﹣2，
综上，平移后抛物线解析式为y=x2+3x+2或y=x2+x﹣2
练习册系列答案
中考解读考点精练系列答案
相关题目
