Question

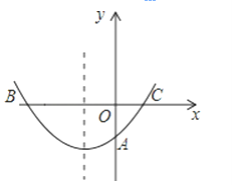
【题目】如图，二次函数y=ax2+bx+c的图象与x轴交于B、C两点，交y轴于点A．

（1）根据图象确定a，b，c的符号；

（2）如果OC=OA=OB，BC=4，求这个二次函数的解析式．

Answer 1

【答案】（1）a＞0，b＞0，c＜0；（2）y=x2+x﹣1．

【解析】

（1）根据抛物线开口方向、对称轴方程以及抛物线与y轴交点的位置确定a，b，c的符号；（2）首先由函数图象可确定A，B，C三点的坐标，然后分别代入二次函数y=ax2+bx+c中即可解得系数，进而即得解析式．

（1）如图，∵抛物线开口方向向上，

∴a＞0．

又∵对称轴x=﹣＜0，

∴a、b同号，即b＞0．

∵抛物线与y轴交与负半轴，

∴c＜0．

综上所述，a＞0，b＞0，c＜0．

（2）如图，∵OC=OA=OB，BC=4，

∴点A的坐标为（0，﹣1），

点B的坐标为（﹣3，0），

点C的坐标为（1，0），

把A，B，C三点分别代入二次函数y=ax2+bx+c中可得：

，

解得，，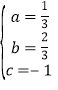

∴该二次函数的解析式是：y=x2+x﹣1．