题目内容
【题目】已知一次函数的图象经过点（﹣2，﹣2）和点（2，4）．
（1）求这个函数的解析式；
（2）判断点P（1，1）是否在此函数图象上，并说明理由．
（3）求这个函数的图象与坐标轴围成的面积．
【答案】（1）y=
x+1；（2）点 P（1，1）不在此函数图象上；（3）
．
【解析】试题分析：（1）使用待定系数法求解析式，设解析式为y=kx+b，然后代入图像中的已知点，得到两个关于k,b的方程，解方程组，问题得解.
(2)把点p代入解析式左右两边，若相等，说明是在图像上，否则不在.
（3）首先要找到与坐标轴的交点，做出图像，找出与坐标轴围城的图形，就可以求面积.其中与y轴交点为（0，b），通过令y=0,得kx+b=0，解方程求出x，即可得到与x轴交点.
解：（1）设一次函数解析式为y=kx+b（k≠0），
将（﹣2，﹣2）、（2，4）代入y=kx+b中，
, 解得：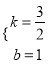 
，
∴这个函数的解析式为
（2）当x=1时， 
∴点 P（1，1）不在此函数图象上．
（3）当x=0时，y=1，
∴该函数图象与y轴交点坐标为（0，1）；
当y=0时，有
，解得： 
，
∴该函数图象与x轴交点坐标为
如图所示，
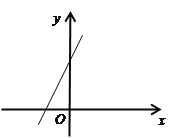
∴这个函数的图象与坐标轴围成的面积
.
练习册系列答案
相关题目
