题目内容
【题目】在平面直角坐标系中,点 A(2,0),B(0,4),点 C 在第一象限.
(1)如图 1,连接 AB、BC、AC,∠OBC=90°,∠BAC=2∠ABO,求点 C 的坐标;
(2)动点 P 从点 B 出发,以每秒 2 个单位的速度沿 x 轴负方向运动,连接 AP,设 P 点的 运动时间为 t 秒,△AOP 的面积为 S,用含 t 的式子表示 S,并直接写出 t 的取值范围;
(3)如图 2,在(1)条件下,点 P 在线段 OB 上,连接 AP、PC,AB 与 PC 相交于点 Q,当S=3, ∠BAC=∠BPC 时,求△ACQ 的面积.
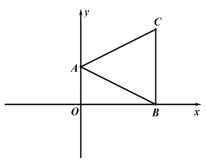
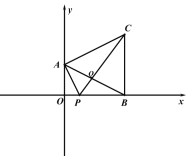
图 1 图 2
【答案】(1)C(4,4);(2)![]() ;(3)
;(3) ![]() .
.
【解析】分析: (1) 作AD⊥BC于D,可得D(4,2),BD=2,根据△ABD≌△ACD,得BC=4,从而
可知C点坐标.
(2)分两种情况根据三角形的面积公式即可求出,一种是当![]() 时,此时点P在OB上;另一种是点P在x轴负半轴上运动时,此时
时,此时点P在OB上;另一种是点P在x轴负半轴上运动时,此时![]() .
.
(3) 作AE⊥PC于E,作BF⊥PC于F,作CG⊥AB于G,可得BP=3,OP=1,由(1)中△ABD≌△ACD得AB=AC,易证△ACE≌△ABO, △AOP≌△AEP,从而得PC=5由面积法,可求BF=2.4,从而AE:BF=5:6由面积法得![]() ,因此
,因此![]() .
.
详解:
(1) 过点A作AD⊥BC于D,
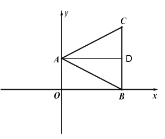
∵点 A(2,0),B(0,4), ∠OBC=90°,
∴D(4,2),
∴BD=2,
∵∠BAC=2∠ABO,
∴∠BAD=∠CAD,
又∵AD=AD, ∠ADB=∠ADC,
∴△ABD≌△ACD,
∴BC=4,
∴C(4,4)
(2)当点P在OB上时,![]() ,
,
由题意得OA=2,OP=4-2t,
∴S=2×(4-2t) ×![]() =4-2t;
=4-2t;
当点P在x轴负半轴上时,![]() ,
,
由题意得OA=2,OP=2t- 4,
∴S=2×(2t- 4) ×![]() =2t- 4;
=2t- 4;
综上,![]()
(3) 作AE⊥PC于E,作BF⊥PC于F,作CG⊥AB于G
∵S=3,
∴可得BP=3,OP=1
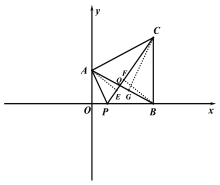
由(1)△ABD≌△ACD
∴AB=AC
∵∠BAC=∠BPC
∴∠ACP=∠ABP
易证△ACE≌△ABO,
△AOP≌△AEP,
∴CE=BO=4,OP=EP=1,
AO=AE=2
∴PC=5(1分)
由面积法,可求BF=2.4
∴AE:BF=5:6
由面积法, ![]()
∴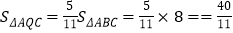

 智慧小复习系列答案
智慧小复习系列答案