题目内容
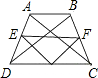
已知等腰梯形的周长为64，腰长为8，对角线长为28，则连接两腰中点与一底中点的线段组成的三角形的周长为______．
∵等腰梯形的周长为64，腰长为8，
∴AB+CD=64-8-8=48，
∵点E，F，G分别是AD，BC，DC的中点，AC=BD=28，
∴EG=FG=
AC=14，EF=
（AB+CD）=24，
∴△EFG的周长=14+14+24=52．
∴AB+CD=64-8-8=48，
∵点E，F，G分别是AD，BC，DC的中点，AC=BD=28，
∴EG=FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴△EFG的周长=14+14+24=52．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
