题目内容
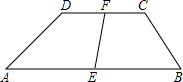
梯形ABCD中,AD∥BC,DE∥AB,对角线BD平分∠ABC,
(1)求证:四边形ABED是菱形.
(2)若∠ABC与∠C互余,BC=8,CD=4,求梯形ABCD的周长.
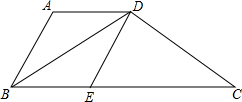
(1)求证:四边形ABED是菱形.
(2)若∠ABC与∠C互余,BC=8,CD=4,求梯形ABCD的周长.

(1)证明:∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∵BD平分∠ABC,
∴∠ABE=∠EBD,
∵AB∥DE,
∴∠ABD=∠BDE,
∴∠EBD=∠BDE,
∴BE=DE,
∴四边形ABDE是菱形;
(2)设AB=x,
∵四边形ABED为菱形,
∴AD=AB=BE=ED=x,
∴CE=BC-BE=8-x,
∵∠DEC=∠ABC,∠ABC+∠C=90°,
∴∠DEC+∠C=90°,
∴∠CDE=90°
∴DE2+CD2=CE2√
∴42+x2=(8-x)2,
∴x=3
∴梯形ABCD的周长=x+x+8+4=18.
∴四边形ABED是平行四边形,
∵BD平分∠ABC,
∴∠ABE=∠EBD,
∵AB∥DE,
∴∠ABD=∠BDE,
∴∠EBD=∠BDE,
∴BE=DE,

∴四边形ABDE是菱形;
(2)设AB=x,
∵四边形ABED为菱形,
∴AD=AB=BE=ED=x,
∴CE=BC-BE=8-x,
∵∠DEC=∠ABC,∠ABC+∠C=90°,
∴∠DEC+∠C=90°,
∴∠CDE=90°
∴DE2+CD2=CE2√
∴42+x2=(8-x)2,
∴x=3
∴梯形ABCD的周长=x+x+8+4=18.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目