题目内容
如图,在△ABC中,∠A=70°,点O是内心,则∠BOC=______.
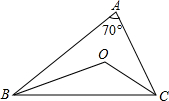

∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°,
∵点O是△ABC的内心,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
故答案为:125°.
∴∠ABC+∠ACB=180°-∠A=110°,
∵点O是△ABC的内心,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
故答案为:125°.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
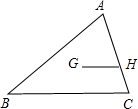
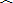
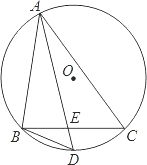
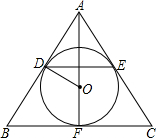 切于点D、E.
切于点D、E.