Question

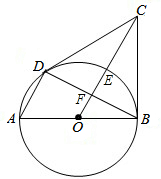
在△ABC中，AB=AC=10，BC=12，AF⊥BC于点F，点O在AF上，⊙O经过点F，并分别与AB、AC边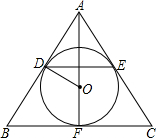切于点D、E．
（1）求△ADE的周长；
（2）求内切圆的面积．

Answer 1

（1）∵AB=AC，BC=12，AF⊥BC于点F，
∴BF=FC=6．
∵⊙O经过点F，并分别与AB、AC边切于点D、E．
∴BD=BF=6，CE=CF=6．
∵AB=AC=10，
∴AD=AE=4，∴AD：AB=AE：AC，∴DE∥BC，
∴DE：BC=AD：AB，即DE：12=4：10，∴DE=4.8，
∴△ADE的周长=AD+DE+AE=4+4+4.8=12.8．

（2）∵AF⊥BC于点F，∴∠AFB=90°．
∵AB=10，BF=6，∴AF=

AB2-BF2

=8．
∵⊙O与AC边切于点D，∴∠ADO=90°．
∴∠ADO=∠AFB，且OD=OF．
∵∠OAD=∠BAF，∴△ADO∽△AFB，
∴AO：AB=OD：BF，
即（8-OD）：10=OD：6，∴OD=3，
∴S_⊙O=π•OD²=9π．