题目内容
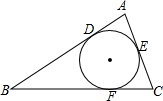
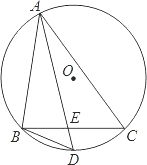
如图，在△ABC的外接圆O中，D是
的中点，AD交BC于点E，连接BD．
（1）列出图中所有相似三角形；
（2）连接DC，若在
上任取一点K（点A，B，C除外），连接CK，DK，DK交BC于点F，DC2=DF•DK是否成立？若成立，给出证明；若不成立，举例说明．
 |
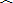| BC |
（1）列出图中所有相似三角形；
（2）连接DC，若在
|
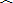| BAC |
（1）△BDE∽△CAE，△DBE∽△DAB，△ABD∽△AEC．
（2）DC2=DF•DK成立．
证明：∵D是
的中点，
∴
=
，
∴∠DBC=∠DCB（等弧的圆周角相等），
又∵∠DBC=∠DKC，
∴∠DCB=∠DKC，
又∵∠KDC=∠CDF，
∴△KDC∽△CDF，
∴
=
，
∴DC2=DF•DK．
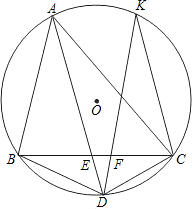
（2）DC2=DF•DK成立．
证明：∵D是
|
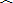| BC |
∴
|
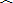| BD |
|
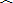| DC |
∴∠DBC=∠DCB（等弧的圆周角相等），
又∵∠DBC=∠DKC，
∴∠DCB=∠DKC，
又∵∠KDC=∠CDF，
∴△KDC∽△CDF，
∴
| KD |
| DC |
| DC |
| DF |
∴DC2=DF•DK．
练习册系列答案
相关题目
