题目内容
【题目】如图所示, 矩形![]() 中,
中,![]() ,
,![]() , 点
, 点![]() 为
为![]() 上一动点(不与端点
上一动点(不与端点![]() 重合) , 连接
重合) , 连接![]() , 将
, 将![]() 沿若
沿若![]() 折叠, 点
折叠, 点![]() 落到
落到![]() 处, 连接
处, 连接![]() ,
,![]() , 若
, 若![]() 为以
为以![]() 为腰的等腰三角形,则
为腰的等腰三角形,则![]() 的长度为__________.
的长度为__________.
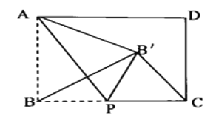
【答案】![]() 或
或![]()
【解析】
当![]() 为以
为以![]() 为腰的等腰三角形时,分两种情况:①BB
为腰的等腰三角形时,分两种情况:①BB![]() =BC=8时,如图2所示,根据折叠的性质得到BO=B
=BC=8时,如图2所示,根据折叠的性质得到BO=B![]() O,根据相似三角形的性质即可得到结论;②CB
O,根据相似三角形的性质即可得到结论;②CB![]() =BC时,连接OC,如图3,由折叠的性质即可得到结论.
=BC时,连接OC,如图3,由折叠的性质即可得到结论.
当![]() 为以
为以![]() 为腰的等腰三角形时
为腰的等腰三角形时
②BB![]() =BC=8时,如图2所示:
=BC=8时,如图2所示:
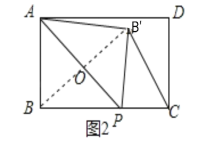
由折叠的性质得BO=B![]() O=
O=![]() BB
BB![]() =4,AP⊥BP,
=4,AP⊥BP,
∴∠AOB=∠ABP=90°,
∵∠BAO=∠BAP,
∴△ABP∽△AOB,
∴![]() ,即
,即![]() ,
,
解得:BP=![]() ;
;
②CB![]() =BC时,连接OC,如图3所示:
=BC时,连接OC,如图3所示:
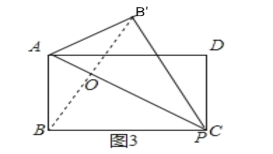
由折叠的性质得:AP垂直平分BB![]() ,
,
∵CB![]() =BC,
=BC,
∴OC⊥BB![]() ,
,
∴点P与C重合,
∴BP=BC=8;
综上所述,当△BB![]() C为等腰三角形时,BP的长为
C为等腰三角形时,BP的长为![]() 或8,
或8,
故答案为:![]() 或8.
或8.

 长江作业本同步练习册系列答案
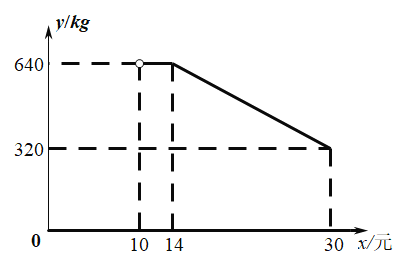
长江作业本同步练习册系列答案【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤,樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤![]() .
.
(1)若小王批发这两种水果正好花费了4400元,那么小王分别购买了多少斤樱桃和榴莲?填写下表,并列方程求解;
品种 | 批发价(元) | 购买斤数 | 小王应付的钱数(元) |
樱桃 | 32 | x | |
榴莲 | 40 |
(2)设小王购买两种水果的总花费为y元,试写出y与x之间的函数表达式.
(3)若要求所批发的榴莲的斤数不少于樱桃斤数的2倍,那么购买樱桃的数量为多少时,可使小王的总花费最少?这个最少花费是多少?
【题目】某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款.某校有4名老师带队,与若干名(不少于4人)学生一起听音乐会.设学生人数为x人,![]() (x为整数).
(x为整数).
(Ⅰ)根据题意填表:
学生人数/人 | 4 | 10 | 20 | … |
方案一付款金额/元 | 80 | 110 | … | |
方案二付款金额/元 | 90 | 117 | … |
(Ⅱ)设方案一付款总金额为![]() 元,方案二付款总金额为
元,方案二付款总金额为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)根据题意填空:
①若用两种方案购买音乐会的花费相同,则听音乐会的学生有________________人;
②若有60名学生听音乐会,则用方案_______________购买音乐会票的花费少;
③若用一种方案购买音乐会票共花费了450元,则用方案________________购买音乐会票,使听音乐的学生人数多.