Question

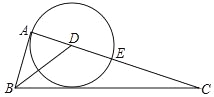
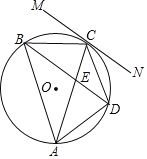
【题目】如图，⊙O为△ABC的外接圆，直线MN与⊙O相切于点C，弦BD∥MN，AC与BD相交于点E．

（1）求证：∠CAB=∠CBD；

（2）若BC=5，BD =8，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）利用切线性质和垂径定理可得=,故∠CAB=∠CBD；

（2）连接OB，在Rt△BCF中，利用勾股定理可得.

解：（1）连接OC，交BD于点F

∵直线MN与⊙O相切于点C，

∴OC ⊥ MN，

∵BD∥ MN，

∴OC ⊥ BD，

∴ =,

∴∠CAB=∠CBD

（2）连接OB

由（1）知OC ⊥ BD，BD=8

∴BF=DF=4

∴在Rt△BCF中得CF=3

设半径为r,在Rt△BOF中，OF=r-3

根据勾股定理可得 解得