题目内容
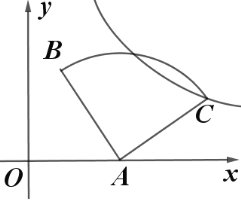
【题目】如图1,点![]() 是
是![]() 的内部一点,连接
的内部一点,连接![]() 、
、![]() 和
和![]() ,如果
,如果![]() 、
、![]() 和
和![]() 中有两个角相等,则称
中有两个角相等,则称![]() 是
是![]() 的“等心”.特别地,若这三个角都相等,则称
的“等心”.特别地,若这三个角都相等,则称![]() 是
是![]() 的“恒等心”.
的“恒等心”.
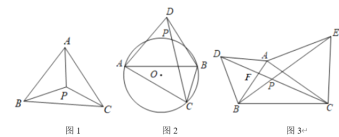
(1)在等边![]() 中,点
中,点![]() 是恒等心,
是恒等心,![]() ,则点
,则点![]() 到
到![]() 的距离是_______;
的距离是_______;
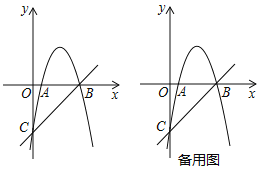
(2)如图2,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的外接圆外一点,连接
的外接圆外一点,连接![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 是不是
是不是![]() 的“等心”,并说明理由;
的“等心”,并说明理由;
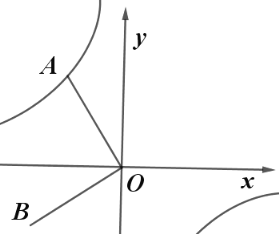
(3)如图3,分别以锐角![]() 的边
的边![]() 、
、![]() 为边向外做等边
为边向外做等边![]() 和等边
和等边![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,求证:点
,求证:点![]() 是
是![]() 的“恒等心”.
的“恒等心”.
【答案】(1)![]() ;(2)
;(2)![]() 是
是![]() 的“等心”,理由见解析;(3)证明见解析.
的“等心”,理由见解析;(3)证明见解析.
【解析】
(1)先根据“恒等心”的定义求出![]() ,再根据三角形全等的判定定理与性质得出
,再根据三角形全等的判定定理与性质得出![]() ,然后根据等腰三角形的性质可得
,然后根据等腰三角形的性质可得![]() ,最后解直角三角形即可得;
,最后解直角三角形即可得;
(2)先根据等腰三角形的性质可得![]() ,再根据圆周角定理可得
,再根据圆周角定理可得![]() ,从而可得
,从而可得![]() ,然后根据领补角的定义、等量代换可得
,然后根据领补角的定义、等量代换可得![]() ,最后根据圆内接四边形的性质可得
,最后根据圆内接四边形的性质可得![]() ,从而可得
,从而可得![]() ,由此即可得证;
,由此即可得证;
(3)如图(见解析),先根据三角形全等的判定定理可得![]() ,从而根据三角形全等的性质可得
,从而根据三角形全等的性质可得![]() ,再根据三角形的外角性质可得
,再根据三角形的外角性质可得![]() ,从而可得
,从而可得![]() ,然后根据相似三角形的判定与性质可得
,然后根据相似三角形的判定与性质可得![]() ,又根据相似三角形的判定与性质可得
,又根据相似三角形的判定与性质可得![]() ,最后根据角的和差可得出
,最后根据角的和差可得出![]() ,由此即可得证.
,由此即可得证.
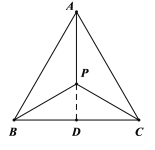
(1)如图,过点P作![]() 于点D
于点D
由“恒等心”的定义得:![]()
![]()
![]()
![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
![]()
在![]() 和
和![]() 中,
中,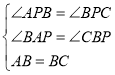
![]()
![]()
![]()
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
即点![]() 到
到![]() 的距离是2
的距离是2
故答案为:![]() ;
;
(2)如图,连接PA、PB
![]()
![]()
由圆周角定理得:![]()
![]()
又![]()
![]()
由圆内接四边形的性质可知,![]()
![]()
![]()
![]() 是
是![]() 的“等心”;
的“等心”;

(3)如图,连接![]()
![]() 和
和![]() 都是等边三角形
都是等边三角形
![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,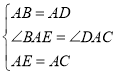
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,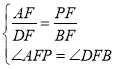
![]()
![]()
![]()
![]()
![]()
则点![]() 是
是![]() 的“恒等心”.
的“恒等心”.


练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目