题目内容
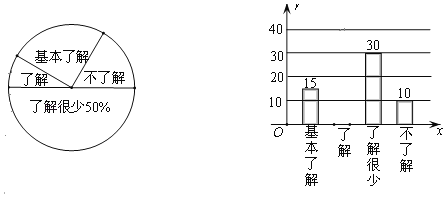
【题目】“食品安全”受到全社会的广泛关注,武汉市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 ;
(2)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,恰好抽到1个男生和1个女生的概率为 ;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
【答案】(1)60;30°;(2)![]() ;(3)估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为300人
;(3)估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为300人
【解析】
(1)用“了解很少”部分的人数除以它所占的百分比可得到调查的总人数;然后用“了解”部分所占的百分比乘以360°得到扇形统计图中“了解”部分所对应扇形的圆心角的度数;
(2)画树状图为(分别用A、B表示两名女生,用C、D表示两名男生)展示所有12种等可能的结果数,再找出恰好抽到1个男生和1个女生的结果数,然后根据概率公式求解;
(3)利用样本估计总体,用900乘以“了解”和“基本了解”所占的百分比的和即可.
(1)30÷50%=60(人),
所以接受问卷调查的学生共有60人;
扇形统计图中“了解”部分所对应扇形的圆心角的度数为![]() ×360°=30°;
×360°=30°;
故答案为60;30°;
(2)画树状图为:(分别用A、B表示两名女生,用C、D表示两名男生)
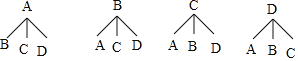
共有12种等可能的结果数,其中恰好抽到1个男生和1个女生的结果数为8,
所以恰好抽到1个男生和1个女生的概率=![]() =
=![]() .
.
故答案为:![]() .
.
(3)900×![]() =300(人),
=300(人),
所以估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为300人;

 天天向上口算本系列答案
天天向上口算本系列答案【题目】某校随机抽查了部分九年级女生进行1分钟仰卧起坐测试,并将测试的结果绘制成了如图的不完整的统计表和频数分布直方图(注:在频数分布直方图中,每组含左端点,但不含右端点):
仰卧起坐次数的范围(次) | 15~20 | 20~25 | 25~30 | 30~35 |
频数 | 3 | 10 | 12 |
|
频率 |
|
|
|
|

(1)30~35的频数是 、25~30的频率是 .并把统计图补充完整;
(2)被抽查的所有女同学仰卧起坐次数的中位数是多少?