Question

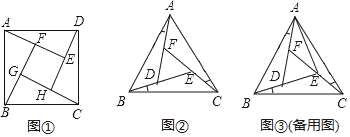
【题目】（1）正方形ABCD，E、F分别在边BC、CD上（不与端点重合），∠EAF＝45°，EF与AC交于点G

①如图（i），若AC平分∠EAF，直接写出线段EF，BE，DF之间等量关系；

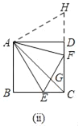
②如图（ⅱ），若AC不平分∠EAF，①中线段EF，BE，DF之间等量关系还成立吗？若成立请证明；若不成立请说明理由

（2）如图（ⅲ），矩形ABCD，AB＝4，AD＝8．点M、N分别在边CD、BC上，AN＝2，∠MAN＝45°，求AM的长度．

Answer 1

【答案】（1）①EF＝BE+DF；见解析；②，①中线段EF，BE，DF之间等量关系还成立：EF＝BE+DF；见解析；（2）AM＝．

【解析】

（1）①结合题意由正方形ABCD的性质得到△ABE≌△ADF，则∠AGE＝∠AGF＝90°，又因为AE平分∠BAC，得到EF＝BE+DF；

②作图延长CD到点H，截取DH＝BE，连接AH，根据已知条件求证△AEB≌△AHD，则AE＝AH，∠BAE＝∠HAD，再证△EAF≌△HAF，则有EF＝HF＝DF+DH＝BE+DF.

（2）根据矩形的性质，和相似△ABN∽△GCN，得到AP＝PM，再设设AP＝x，最终求得

AM．

（1）①如图（i），

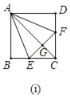
∵四边形ABCD是正方形，

∴∠BAC＝∠CAD＝45°，

∵∠EAF＝45°，AC平分∠EAF，

∴∠BAE＝∠EAG＝∠DAF＝∠FAG＝22.5°，

∵AB＝AD，∠B＝∠D＝90°，

∴△ABE≌△ADF（ASA），

∴BE＝DF，AE＝AF，

∴∠AEF＝∠AFE，

∴AC⊥EF，

∴∠AGE＝∠AGF＝90°，

∵AE平分∠BAC，

∴BE＝EG，DF＝GF，

∴EF＝BE+DF；

②，①中线段EF，BE，DF之间等量关系还成立：EF＝BE+DF；

如图（ⅱ），延长CD到点H，截取DH＝BE，连接AH，

在△AEB与△AHD中，

∵，

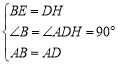∴△AEB≌△AHD（SAS），

∴AE＝AH，∠BAE＝∠HAD，

∵∠EAF＝45°，∠BAD＝90°，

∴∠BAE+∠DAF＝45°，

∴∠DAF+∠DAH＝45°．即∠EAF＝∠HAF，

在△EAF与△HAF中，

∵，

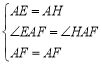∴△EAF≌△HAF（SAS），

∴EF＝HF＝DF+DH＝BE+DF，

（2）如图（iii），延长AN，DC交于点G，过M作MP⊥AG于点P，

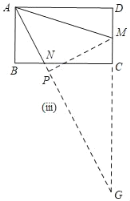
∵四边形ABCD是矩形，

∴∠B＝90°，

Rt△ABN中，AB＝4，AN＝2，

∴BN＝2，CN＝8﹣2＝6，

∵AB∥CG，

∴△ABN∽△GCN，

∴，

∴NG＝6，

∵∠MAN＝45°，∠APM＝90°，

∴AP＝PM，

设AP＝x，则PM＝2x，PG＝2x，

∵AG＝2+6＝x+2x，

x＝，

∴AM＝x＝．