题目内容
【题目】已知正方形ABCD中,P为直线AD上一点,以PD为边做正方形PDEF,使点E在线段CD的延长线上,连接AC、AF.若![]() ,则
,则![]() 的度数为________.
的度数为________.
【答案】![]() 或
或![]()
【解析】
根据题意需要分三种情况讨论计算:(1)当点P在DA的延长线上时,因为AD<PD,与条件不符,所以这种情况不成立;(2)当点P在线段DA上时,连接FD,根据已知条件和正方形的性质可得△ADF是等腰三角形,顶角是45°,求出底角,从而求解;(3)当点P在AD的延长线上时,连接FD,方法同(2)即可解答.
解:(1)当点P在DA的延长线上时,AD<PD,不符合![]() ,故这种情况不成立;
,故这种情况不成立;
(2)当点P在线段DA上时,如图:
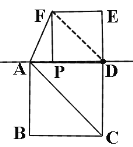
连接FD,∵正方形PDEF中,FD=![]() PD,
PD, ![]() ,∠ADF=45°,
,∠ADF=45°,
∴FD=AD,∠DAF=∠AFD=(180°-45°)÷2=67.5°,
∴![]() =∠CAD+∠DAF=45°+67.5°=
=∠CAD+∠DAF=45°+67.5°=![]() ;
;
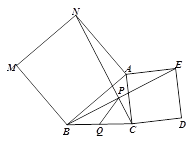
(3))当点P在AD的延长线上时,如图:
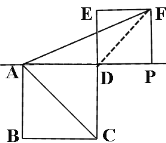
连接FD,∵正方形PDEF中,FD=![]() PD,
PD, ![]() ,∠PDF=45°=∠FAD+∠DFA,
,∠PDF=45°=∠FAD+∠DFA,
∴AD=DF,∠FAD=∠DFA =45°÷2=22.5°,
∴![]() =∠CAD+∠DAF=45°+22.5°=67.5°;
=∠CAD+∠DAF=45°+22.5°=67.5°;
故答案为:![]() 或
或![]()

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目