题目内容
【题目】【问题背景】
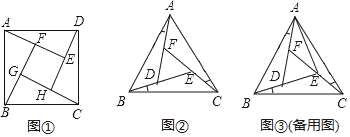
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.
【答案】(1)△ABD≌△BCE≌△CAF;理由见解析;(2)△DEF是正三角形;理由见解析;(3)![]()
【解析】分析:(1)由正三角形的性质得出∠CAB=∠ABC=∠BCA=60°,AB=BC,证出∠ABD=∠BCE,由ASA证明△ABD≌△BCE即可;
(2)由全等三角形的性质得出∠ADB=∠BEC=∠CFA,证出∠FDE=∠DEF=∠EFD,即可得出结论;
(3)先判断出AF=FD=EF,进而得出∠FAE=∠FEA=30°,即:∠DEA=90°,再用勾股定理得出AE,即可得出结论.
详解:(1)△ABD≌△BCE≌△CAF;理由如下:
∵△ABC是正三角形,
∴∠CAB=∠ABC=∠BCA=60°,AB=BC,
∵∠ABD=∠ABC-∠CBE,∠BCE=∠ACB-∠ACF,∠CBE=∠ACF,
∴∠ABD=∠BCE,
在△ABD和△BCE中,
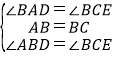 ,
,
∴△ABD≌△BCE(ASA);
同理:△ABD≌CAF,
即:△ABD≌△BCE≌△CAF
(2)△DEF是正三角形;理由如下:
∵△ABD≌△BCE≌△CAF,
∴∠ADB=∠BEC=∠CFA,
∴∠FDE=∠DEF=∠EFD,
∴△DEF是正三角形;
(3)∵△DEF是正三角形,
∴∠DFE=∠FDE=60°,
又AF=FD,
∴AF=FD=EF,
∴∠FAE=∠FEA=30°,
∴∠DEA=90°,
设DE=x,则AD=BE=2x,
在Rt△ADE中,AE2=AD2-DE2=3x2,
在Rt△ABE中,AB=7,AB2=BE2+AE2,
即,49=4x2+3x2,
∴x=-![]() (舍)或x=
(舍)或x=![]() ,
,
∴△DEF的边长为![]() .
.