题目内容
【题目】如图,将线段AB绕点A逆时针旋转α度角得到线段AC,将线段AB绕点B逆时针旋转α度角得到线段BD(0°<α<180°),连结BC、AD.当α=_______度时,四边形ACBD是菱形,并说明理由.
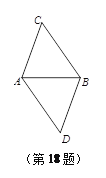
【答案】60
【解析】分析:根据旋转的性质得到AC=AB,∠CAB=60°.判定△ABC为等边三角形.
进一步判定四边形ACBD是平行四边形.根据AC=BC,即可判定四边形ACBD是菱形.
详解:60
理由如下:
∵线段AB绕点A逆时针旋转60°得到线段AC,
∴AC=AB,∠CAB=60°.
∴△ABC为等边三角形.
∴AC=BC.
∵线段AB绕点B逆时针旋转60°得到线段BD,
∴BD=AB,∠ABD=60°.
∴AC=BD,∠CAB=∠ABD.
∴AC∥BD.
∴四边形ACBD是平行四边形.
∵AC=BC,
∴四边形ACBD是菱形.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目