题目内容
【题目】某牛奶厂在一条南北走向的大街上设有O,A,B,C四家特约经销店.A店位于O店的南面3千米处;B店位于O店的北面1千米处,C店在O店的北面2千米处.
(1)请以O为原点,向北的方向为正方向,1个单位长度表示1千米,画一条数轴,你能在数轴上分别表示出O,A,B,C的位置吗?
(2)牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店,那么送货车走的最短路程是多少千米?
【答案】(1)能,图见解析;(2)送货车走的最短路程是7千米
【解析】
(1)根据题意以O为原点,向北的方向为正方向,1个单位长度表示1千米可画出数轴, 再根据A店位于O店的南面3千米处,可确定A位于O点左边距离原点O 3个单位,即表示-3,B店位于O店的北面1千米处,可确定点B位于点O右边距离原点1个单位,即表示为1,C店在O店的北面2千米处, 可确定点B位于点O右边距离原点2个单位,即表示为2,
(2) 牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店, 送货车走的最短路程是从点O到B再到点C再到点A,即2-(-3)+2,然后计算即可求解.
解:(1)能,如图所示:
![]()
(2)依题意得最短路程为2-(-3)+2=7(千米).
答:送货车走的最短路程是7千米.

【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式. 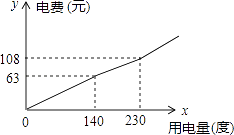
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费元;
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.