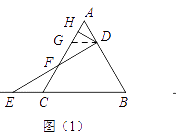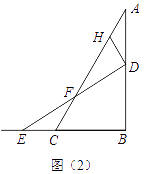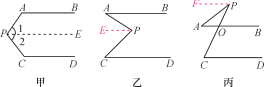题目内容
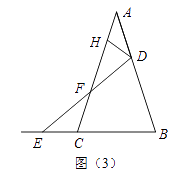
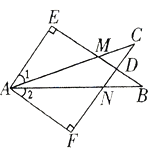
【题目】如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
【答案】①②③
【解析】
∠E=∠F=90°,∠B=∠C,AE=AF可得△ABE≌△ACF,三角形全等的性质BE=CF;∠BAE=∠CAF可得①∠1=∠2;由ASA可得△ACN≌△ABM.④CD=DN不成立.
解:∵∠E=∠F=90°,∠B=∠C,AE=AF
∴△ABE≌△ACF
∴BE=CF
∠BAE=∠CAF
∠BAE-∠BAC=∠CAF-∠BAC
∴∠1=∠2
△ABE≌△ACF
∴∠B=∠C,AB=AC
又∠BAC=∠CAB
△ACN≌△ABM.
④CD=DN不能证明成立,3个结论对.
故答案是:①②③

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目