Question

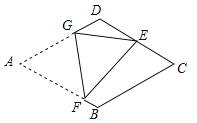
【题目】如图，O是等边内一点，,以点B为旋转中心，将线段BO逆时针旋转得到线段，连接，则下列结论：

①可以由绕点B逆时针旋转得到

②连接，则

③

④

其中正确的结论是____________．

Answer 1

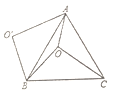
【答案】①②③

【解析】

如图，连接OO′，首先证明△OBO′为为等边三角形，得到OO′＝OB＝4，故选项②正确；证明△ABO′≌△CBO，得到选项①正确；运用勾股定理逆定理证明△AOO′为直角三角形，求出∠AOB的度数，得到选项③正确；运用三角函数及三角形面积公式求出四边形AOBO′的面积，可判断选项④错误．

解：如图，连接OO′；

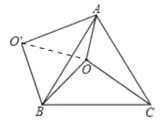
∵△ABC为等边三角形，

∴∠ABC＝60°，AB＝CB，

由题意得：∠OBO′＝60°，OB＝O′B，

∴△OBO′为等边三角形，∠ABO′＝∠CBO，

∴OO′＝OB＝4，∠BOO′＝60°，②正确；

在△ABO′与△CBO中，，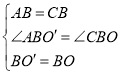

∴△ABO′≌△CBO（SAS），

∴AO′＝OC＝5，

∴△BO′A可以由△BOC绕点B逆时针方向旋转60°得到，①正确；

在△AOO′中，AO′＝5，OA＝3，OO′＝4，

∵32＋42＝52，

∴△AOO′为直角三角形，且∠AOO′＝90°，

∴∠AOB＝90°＋60°＝150°，③正确；

∵S四边形AOBO′＝×4×4×sin60°＋×3×4＝，④错误，

综上所述，正确的结论为①②③．

故答案为：①②③．