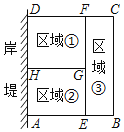
题目内容
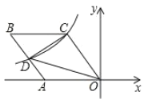
【题目】如图,正方形ABCD的边长为![]() ,E,F分别是AB,BC的中点,AF与DE,DB分别交于点M,N,则△DMN的面积= .
,E,F分别是AB,BC的中点,AF与DE,DB分别交于点M,N,则△DMN的面积= .
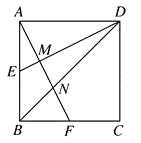
【答案】8.
【解析】
首先连接DF,由四边形ABCD是正方形,可得△BFN∽△DAN,又由E,F分别是AB,BC的中点,可得![]() =2,△ADE≌△BAF(SAS),然后根据相似三角形的性质与勾股定理,可求得AN,MN的长,即可得MN:AF的值,再利用同高三角形的面积关系,求得△DMN的面积.
=2,△ADE≌△BAF(SAS),然后根据相似三角形的性质与勾股定理,可求得AN,MN的长,即可得MN:AF的值,再利用同高三角形的面积关系,求得△DMN的面积.
连接DF,
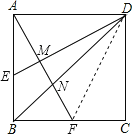
∵四边形ABCD是正方形,
∴AD∥BC,AD=BC=![]() ,
,
∴△BFN∽△DAN,
∴![]() ,
,
∵F是BC的中点,
∴![]() ,
,
∴AN=2NF,
∴![]() ,
,
在Rt△ABF中![]() ,
,
∴![]() ,
,
∵E,F分别是AB,BC的中点,AD=AB=BC,
∴![]() ,
,
∵∠DAE=∠ABF=90°,
在△ADE与△BAF中,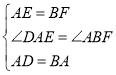 ,
,
∴△ADE≌△BAF(SAS),
∴∠AED=∠AFB,
∴∠AME=180°-∠BAF-∠AED=180°-∠BAF-∠AFB=90°.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .
.
故答案为:8.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目