Question

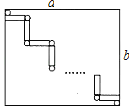
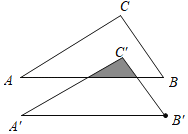
【题目】如图，将Rt△ABC平移到△A'B'C'的位置，其中∠C＝90°使得点C'与△ABC的内心重合，已知AC＝4，BC＝3，则阴影部分的面积为（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

由三角形面积公式可求C'E的长，由相似三角形的性质可求解．

如图，过点C'作C'E⊥AB，C'G⊥AC，C'H⊥BC，并延长C'E交A'B'于点F，连接AC'，BC'，CC'，

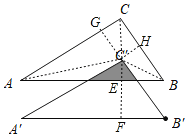
∵点C'与△ABC的内心重合，C'E⊥AB，C'G⊥AC，C'H⊥BC，

∴C'E=C'G'=C'H，

∵S△ABC=S△AC'C+S△AC'B+S△BC'C，

∴AC×BC=AC×CC'+BA×C'E+BC×C'H

∴C'E=1，

∵将Rt△ABC平移到△A'B'C'的位置，

∴AB∥A'B'，AB=A'B'，A'C'=AC=4，B'C'=BC=3

∴C'F⊥A'B'，A'B'=5

∴A'C'×B'C'=A'B'×C'F

∴C'F=

∵AB∥A'B'

∴△C'MN∽△C'A'B'，

∴S阴影部分=S△C'A'B'×（）2，

∴S阴影部分=×4×3×＝

故选：D．