题目内容
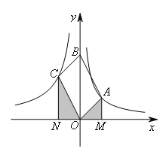
【题目】(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
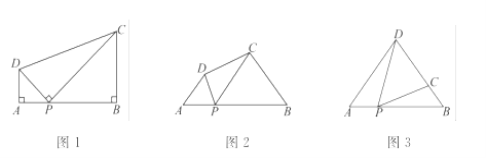
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
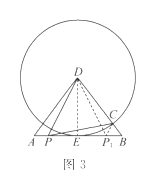
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
【答案】(1)见解析; (2)结论AD·BC=AP·BP仍成立.理由见解析;(3)t的值为2秒或10秒.
【解析】
(1)由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证得△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(2)由∠DPC=∠A=∠B=θ可得∠ADP=∠BPC,即可证得△ADP∽△BPC,然后运用相似三角形的性质即可解决问题;
(3)过点D作DE⊥AB于点E,根据等腰三角形的性质可得AE=BE=6,根据勾股定理可得DE=8,由题意可得DC=DE=8,则有BC=108=2,易证∠DPC=∠A=∠B,根据AD·BC=AP·BP,即可求出t的值.
(1)证明:∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,∠BPC+∠APD=90°,
∴∠ADP=∠BPC,
∴△ADP∽△BPC,
∴![]() ,
,
∴AD·BC=AP·BP;
(2)结论AD·BC=AP·BP仍成立
理由:∵∠BPD=∠DPC+∠BPC,且∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADP,
∵∠DPC=∠A=θ,
∴∠BPC=∠ADP,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴![]() ,
,
∴AD·BC=AP·BP;
(3)如图3,过点D作DE⊥AB于点E,
∵AD=BD=10,AB=12,.
∴AE=BE=6,
∴![]() ,
,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=8,
∴BC=10-8=2,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得AD·BC=AP·BP,
又∵AP=t,BP=12-t,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
∴t的值为2秒或10秒.

【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球,放回、搅匀,下表是活动进行中的一组统计数据,
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.230 | 0.231 | 0.300 | 0.260 | 0.254 |
袋中白球的个数约为______.