题目内容
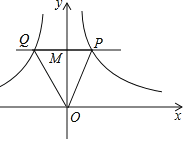
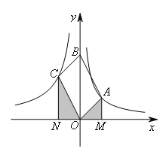
【题目】如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限内的点C分别在双曲线![]() 和
和![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
①阴影部分的面积为![]() ;
;
②若B点坐标为(0,6),A点坐标为(2,2),则![]() ;
;
③当∠AOC=![]() 时,
时,![]() ;
;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是 ____________(填写正确结论的序号).
【答案】②④
【解析】
由题意作AE⊥y轴于点E,CF⊥y轴于点F,①由S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,得到S阴影部分=S△AOM+S△CON=
|k2|,得到S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|)=
(|k1|+|k2|)=![]() (k1-k2);
(k1-k2);
②由平行四边形的性质求得点C的坐标,根据反比例函数图象上点的坐标特征求得系数k2的值.
③当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;④若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,同时也关于y轴对称.
解:作AE⊥y轴于E,CF⊥y轴于F,如图:

∵S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,得到S阴影部分=S△AOM+S△CON=
|k2|,得到S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|);
(|k1|+|k2|);
而k1>0,k2<0,
∴S阴影部分=![]() (k1-k2),故①错误;
(k1-k2),故①错误;
②∵四边形OABC是平行四边形,B点坐标为(0,6),A点坐标为(2,2),O的坐标为(0,0).
∴C(-2,4).
又∵点C位于y=![]() 上,
上,
∴k2=xy=-2×4=-8.
故②正确;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,故③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=-k2,
∴两双曲线既关于x轴对称,也关于y轴对称,故④正确.
故答案是:②④.