题目内容
【题目】如图,∠AOC=140°,OD平分∠AOC,OE平分∠BOC.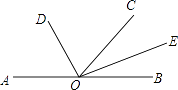
(1)求∠BOE的度数.
(2)求∠DOE的度数.
【答案】
(1)解:∵∠AOC=140°,
∴∠COB=180°﹣140°=40°,
∵OE平分∠BOC,
∴∠BOE= ![]() ∠BOC=20°
∠BOC=20°
(2)解:∵∠AOC=140°,OD平分∠AOC,
∴ ![]() =
= ![]() =70°,
=70°,
∵∠COE=∠BOE=20°,
∴∠DOE=∠DOC+∠COE=70°+20°=90°
【解析】(1)根据平角的定义得出∠COB=180°﹣140°=40°,然后根据角平分线线的定义得出∠BOE= ![]() ∠BOC=20° ;
∠BOC=20° ;
(2)根据角平分线线的定义得出∠ D O C = ![]() ∠ A O C =
∠ A O C = ![]() × 140 =70°,∠COE=∠BOE=20°,然后根据角的和差得出∠DOE=∠DOC+∠COE=70°+20°=90° 。
× 140 =70°,∠COE=∠BOE=20°,然后根据角的和差得出∠DOE=∠DOC+∠COE=70°+20°=90° 。

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
【题目】已知某司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行),某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
(1)现在该公司收购了140吨蔬菜,如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,然后进行粗加工,要求15天刚好加工完140吨蔬菜,则应如何分配加工时间?