题目内容
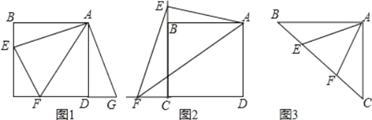
【题目】已知，在正方形ABCD中，E是CB延长线上一点，且EB=
BC，F是AB的中点，请你将F点与图中某一标明字母的点连接成线段，使连成的线段与AE相等．并证明这种相等关系．
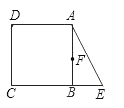
【答案】解：如图，连接DF、CF均可得出与AE相等．
证明：∵ABCD为正方形，
∴AD=AB，∠DAF=∠ABE，
∵F为中点，BE=
BC，
∴AF=BE，
∴△ADF≌△BAF，
∴DF=AE．
同理可得CF=AE．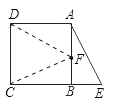
【解析】根据题意可以知道连接CF、DF均可，可以根据三角形全等证明．
【考点精析】本题主要考查了正方形的性质的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】小林在某店购买A、B商品共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，三次购买商品A、B的数量和费用如下表：
购买商品A的数量（个） | 购买商品B的数量（个） | 购买总费用（元） | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
（1）小林以折扣价购买商品A、B是第次购物；
（2）求出商品A、B的标价；
（3）若商品A、B的折扣相同，问商店是打几折出售这两种商品的？
