题目内容
【题目】如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始以2cm/秒的速度移动,点Q沿DA边从D以1cm/秒的速度移动,若P、Q同时出发,用t表示移动时间(0≤t≤6),求当t何值时,△APQ与△ABC相似? 
【答案】解:由题意得:AP=2tcm,DQ=tcm,则AQ=(6﹣t)cm, ∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
在△ABD和△BAC中,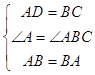 ,
,
∴△ABD≌△BAC(SAS),
若△APQ与△ABC相似,则△APQ与△ABD相似;
分两种情况:
① 当 ![]() 时,
时,
即 ![]() ,
,
解得:t=3;
②当 ![]() 时,
时,
即 ![]() ,
,
解得:t= ![]() .
.
综上所述:当t=3或t= ![]() 时,△APQ与△ABC相似
时,△APQ与△ABC相似
【解析】由矩形的性质和SAS证出△ABD≌△BAC,若△APQ与△ABC相似,则△APQ与△ABD相似;分两种情况:①当 ![]() 时;②当
时;②当 ![]() 时;分别得出t的方程,解方程即可.
时;分别得出t的方程,解方程即可.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对相似三角形的判定的理解,了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

练习册系列答案
相关题目