��Ŀ����
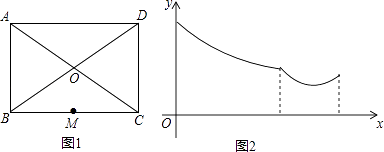
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A��2��0������OAΪһ���ڵ��������ڻ�������OABC��D��m��0��Ϊx���ϵ�һ�����㣨m��2������BDΪһֱ�DZ��ڵ��������ڻ�����ֱ����BDE��������DBE=90�㣮
��1�����ж��߶�AE��CD��������ϵ����˵�����ɣ�
��2����DE���е�ΪF��ֱ��AF��y���ڵ�G���ʣ����ŵ�D���˶�����G��λ���Ƿ�ᷢ���仯�������ֲ��䣬�������G�����ꣻ�������仯����˵�����ɣ�
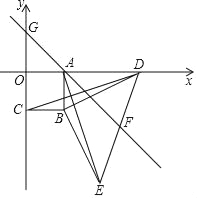
���𰸡���1��AE=CD�����������������2����G��λ�ò��ᷢ���仯���������������
��������
��1����������OABC���ɵ�BC=BA����ABC=90�����ɵ���ֱ��������BDE���ɵ�BD=BE����DBE=90�����ٸ��ݡ�CBD=��ABE�����ɵõ���CBD�ա�ABE�������ó�CD=AE��
��2������E��PQ��OD���ֱ�ֱ��AB��AF�ڵ�P��Q���ж���ADB�ա�PBE���ɵ�AD=PB��AB=PE���ж���ADF�ա�QEF���ɵ�AD=QE������AP=QP���ɵá�AQP=45��������PQ��OD���ɵá�OAG=��Q=45���������õ���AOG�ǵ���ֱ�������Σ������õ�G��0��2��������G��λ�ò��ᷢ���仯��
��1��AE=CD��
���ɣ���������OABC���ɵ�BC=BA����ABC=90�㣬
�ɵ���ֱ��������BDE���ɵ�BD=BE����DBE=90�㣬
���ABC+��ABD=��DBE+��ABD��
����CBD=��ABE��
���CBD�ա�ABE��
��CD=AE��
��2����G��λ�ò��ᷢ���仯��
���ɣ���ͼ������E��PQ��OD���ֱ�ֱ��AB��AF�ڵ�P��Q��
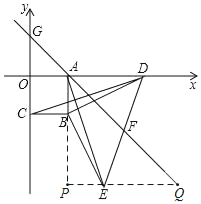
�ߡ�DAB=��P=��DBE=90�㣬
���ADB+��ABD=��PBE+��ABD=90�㣬
���ADB=��PBE��
�֡�DB=BE��
���ADB�ա�PBE��
��AD=PB��AB=PE��
��F��DE���е㣬
��DF=EF��
��AD��EQ��
���DAF=��Q��
�֡ߡ�AFD=��QFE��
���ADF�ա�QEF��
��AD=QE��
��AB+BP=PE+EQ����AP=QP��
���AQP=45�㣬
�֡�PQ��OD��
���OAG=��Q=45�㣬
���AOG�ǵ���ֱ�������Σ�
��GO=AO=2��
��G��0��2��������G��λ�ò��ᷢ���仯��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ���Ķ����в��ϣ�
�������Ϲ����˿����仯������ᾭ�ú�������ᵽ�ı�����һ�����һ����65 �꼰���������˿�����ռ���˿ڱ�������7%ʱ����ζ��������һ�����������仯���Ӿ��ýǶȣ�һ����á������˿ڸ����ȡ�����ӳ�˿����仯���ĺ������ν�������˿ڸ����ȡ���ָij��Χ�˿��У������˿�����65 �꼰�����˿��������Ͷ������˿�����15��64 ���˿�����֮�ȣ�ͨ���ðٷֱȱ�ʾ�����Ա���ÿ100 ���Ͷ������˿�Ҫ���������������ˣ�
�����Ǹ����ҹ���������˿��������������ͳ��ͼ��ͳ�Ʊ���
2011��2014 ��ȫ���˿�����ֲ�ͼ
2011��2014 ��ȫ���˿�����ֲ���
2011�� | 2012�� | 2013�� | 2014�� | |
0��14���˿�ռ���˿ڵİٷֱ� | 16.4% | 16.5% | 16.4% | 16.5% |
15��64���˿�ռ���˿ڵİٷֱ� | 74.5% | 74.1% | 73.9% | 73.5% |
65�꼰�����˿�ռ���˿ڵİٷֱ� | m | 9.4% | 9.7% | 10.0% |
�������ϲ��Ͻ���������⣺
��1��2011 ��ĩ���ҹ����˿�ԼΪ�ڣ�ȫ���˿�����ֲ�����m��ֵΪ��
��2������Ŀǰ�ҹ����˿���Ȼ�������Ʋ⣬��2027 ��ĩ�ҹ�Լ��14.60 ���ˣ�����0��14���˿�ռ���˿ڵİٷֱ�һֱ�ȶ���16.5%��15��64���˿�һֱ�ȶ���10 �ڣ���ô2027 ��ĩ�ҹ�0��14���˿�ԼΪ�ڣ��������˿ڸ����ȡ�ԼΪ������ȷ��1%��
��3��2016 ��1 ��1 �����ҹ���ʼʵʩ��ȫ���̥�����ߣ�һ�Է��������������ӣ���δ��10���ڣ����������������ߣ�������ᡱ���ᡱ�����ҹ��ġ������˿ڸ����ȡ�����Ӱ�죮