Question

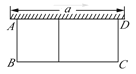
【题目】如图，有一个长为24米的篱笆，一面利用墙（墙的最大长度a为15米）围成的中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米．

（1）求S与x的函数关系式；

（2）如果要使围成花圃面积最大，求AB的长为多少米？

Answer 1

【答案】（1）S-3x2+24x；（2）当AB长为4m，宽为12m时，有最大面积，为48平方米．

【解析】

（1）可先用篱笆的长表示出BC的长，然后根据矩形的面积=长×宽，得出S与x的函数关系式；

（2）根据二次函数的性质求出自变量取值范围内的最值．

（1）S=（24-3x）x =-3x2+24x

（2）S=（24-3x）x =-3x2+24x =-3（x-4）2+48，

∴当AB长为4m，宽为12m时，有最大面积，为48平方米．