题目内容
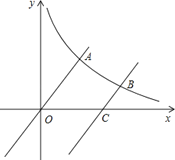
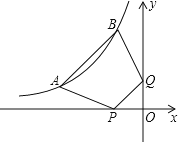
【题目】如图，点A（a，1），B（b，3）都在双曲线y＝﹣
上，点P，Q分别是x轴，y轴上的动点，则四边形ABPQ周长的最小值为（ ）
A.4
B.6C.2
+2D.8
【答案】B
【解析】
先把A点和B点的坐标代入反比例函数解析式中，求出a与b的值，确定出A与B坐标，再作A点关于x轴的对称点D，B点关于y轴的对称点C，根据对称的性质得到C点坐标为(1，3)，D点坐标为(-3，-1)，CD分别交x轴、y轴于P点、Q点，根据两点之间线段最短得此时四边形ABPQ的周长最小，然后利用两点间的距离公式求解可得．
解：∵点A(a，1)，B(b，3)都在双曲线y＝﹣
上，
∴a×1＝3b＝﹣3，
∴a＝﹣3，b＝﹣1，
∴A(﹣3，1)，B(﹣1，3)，
作A点关于x轴的对称点D(﹣3，﹣1)，B点关于y轴的对称点C(1，3)，连接CD，分别交x轴、y轴于P点、Q点，此时四边形ABPQ的周长最小，
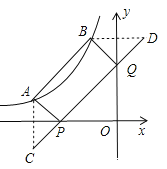
∵QB＝QC，PA＝PD，
∴四边形ABPQ周长＝AB+BQ+PQ+PA＝AB+CD，
∴AB＝
＝2
，CD＝
＝4，
∴四边形ABPQ周长最小值为2+4＝6，
故选：B．
小学夺冠AB卷系列答案
ABC考王全优卷系列答案【题目】在5月31日世界禁烟日到来之际，某校为了提高禁烟意识，在七、八年级举办了“关爱健康，远离香烟”的知识竞赛，两个年级分别有500人为了了解本次竞赛成绩情况，现从中各随机抽取了部分同学的测试成绩x（得分均为整数，满分为100分）进行调查分析，过程如下：
第一步：收集数据
七年级：68 88 100 100 79 94 89 85 100 88 81 69 98 79 77 94 96 75 92 67
八年级：69 97 78 89 98 100 99 100 95 99 99 69 75 100 99 78 79 87 85 79
第二步：整理、描述数据
分数段 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x≤100 |
七年级人数 | 3 | 4 | 5 | 8 |
八年级人数 | 2 | 5 | 3 | 10 |
第三步：分析数据
年级 | 平均数 | 中位数 | 众数 | 满分率 | 方差 |
七年级 | 86 | 88 | 100 | 15% | 115．6 |
八年级 | 88．7 | 92 | a | 15% | 120 |
第四步：应用数据
（1）直接写出a的值和八年级抽取了多少个同学的成绩进行分析
（2）在此次测试中，七年级甲学生的成绩为89分，八年级乙学生成绩为90分，甲、乙两人的成绩在各自年级中哪一个更靠前？请说明理由．
（3）若成绩在90分至99分之间（含90分，99分）的学生为二等奖，请估计七、八年级一共获得二等奖的学生总人数．
