题目内容
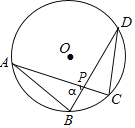
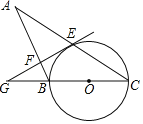
【题目】如图,BC是⊙O的直径,CE是⊙O的弦,过点E作⊙O的切线,交CB的延长线于点G,过点B作BF⊥GE于点F,交CE的延长线于点A.
(1)求证:∠ABG=2∠C;
(2)若GF=3![]() ,GB=6,求⊙O的半径.
,GB=6,求⊙O的半径.
【答案】(1)见解析;(2)6
【解析】
(1)连接OE,根据切线的性质得到OE⊥EG,推出OE∥AB,得到∠A=∠OEC,根据等腰三角形的性质得到∠OEC=∠C,求得∠A=∠C,根据三角形的外角的性质即可得到结论;
(2)根据勾股定理得到BF=![]() =3,根据相似三角形的性质即可得到结论.
=3,根据相似三角形的性质即可得到结论.
证明:(1)如下图:连接OE,
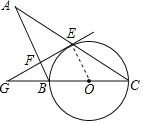
∵EG是⊙O的切线,
∴OE⊥EG,
∵BF⊥GE,
∴OE∥AB,
∴∠A=∠OEC,
∵OE=OC,
∴∠OEC=∠C,
∴∠A=∠C,
∵∠ABG=∠A+∠C,
∴∠ABG=2∠C;
解:(2)∵BF⊥GE,
∴∠BFG=90°,
∵GF=3![]() ,GB=6,
,GB=6,
∴BF=![]() =3,
=3,
∵BF∥OE,
∴△BGF∽△OGE,
∴![]() ,
,
∴![]() ,
,
∴OE=6,
∴⊙O的半径为6.

练习册系列答案
相关题目